
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дисперсии и стандартные ошибки коэффициентов
|
|
Для анализа статистической значимости полученных коэффициентов множественной линейной регрессии необходимо определить существенность коэффициентов регрессии a 1,..., a m..
Дляоценить дисперсию и стандартные отклонения коэффициентов a, a 1,..., a m .
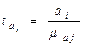 | |||
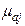 |
Для определения - ошибки j-го коэффициента регрессии надо рассчитать дисперсии и стандартные отклонения по Х и по Y
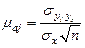
Где n – количество наблюдений
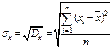 | ||
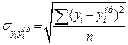 |
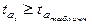 Производим сравнение
Производим сравнение
После построения уравнения регрессии возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии, что делают с помощью t-критерия Стьюдента. Расчетные значения данного показателя сравнивают с критическими, которые определяют по таблице с учетом принятого уровня значимости (a = 0, 10; a = 0, 05 или a = 0, 01) (при изучении социально-экономических явлений достаточным считается уровень значимости, равный 0, 05) и числа степеней свободы n = n – m – 1 (где n – число наблюдений; m – число факторов уравнения, включая результативный). Параметр признается значимым, если tрасч. ³ tтабл.
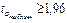
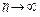 Упрощение:
Упрощение:
Если есть коэффициент регрессии, для которого условие не выполняется, то из уравнения исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение t -критерия. После этого уравнение регрессии строится без исключенного фактора и снова проверяется значимость коэффициентов регрессии. Такой процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в уравнении только существенных (действительно влияющих на результативный показатель) факторов.
Иногда расчетные значения t-критерия ниже критического значения для факторных признаков, имеющих достаточно тесную связь с результативным. Это связано с проявлением эффекта мультиколлинеарности, когда два и более признака, оказывающих влияние на результативный, тесно связаны друг с другом. В таком случае включение одного из них (наиболее значимого) в уравнение регрессии позволяет учесть и влияние других.
Эти вычисления достаточно трудоемки. Разумеется, эти процедуры уже реализованы в том или ином виде, в каждом пакете прикладных программ, предназначенном для обработки статистических данных. Например, при использовании Excel будут получены:
· Коэффициенты a, a 1,..., a m ;
· Стандартные ошибки для этих коэффициентов;
· t -статистики (отношение величины коэффициента к его стандартной ошибке);
· p -значения, рассчитанные на основе t -статистики имеющей распределение Стьюдента с N-m- 1степенями свободы;
· Нижние и верхние границы (интервальные оценки коэффициентов уравнения регрессии) для заданной вероятности (по умолчанию 95%).
Если число степеней свободы, достаточно велико (не менее 8-10), то при 5%-ном уровне значимости и двусторонней альтернативной гипотезе критическое значение t -статистики приблизительно равно двум. Здесь, как и в случае парной регрессии, можно приближенно считать оценку незначимой, если t -статистика по модулю меньше единицы, и весьма надежной, если модуль t -статистики больше трех.