
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка общего качества уравнения регрессии
|
|
*** Рассмотрим методику проверки общего качества построенной многофакторной корреляционной модели (без использования компьютера):
Для определения тесноты связи используется коэффициент множественной корреляции R
 |
упр это расчетное значение результативного показателя
уi это фактическое значение результативного показателя
уср среднее фактических значений результативного показателя
| № | факт уi | расчет по модели упр |
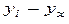
| ||
| … | ||
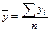 |
Таким образом, в числителе формулы имеем выражение, определяющее необъяснимую вариацию:
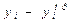 |
Чем совершеннее модель, тем упр ближе к уi
В идеале
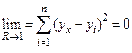 | ||
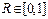 |
После определения коэффициента корреляции требуется определить его существенность (надежность)
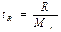 | ||
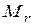 |
это ошибка соответствующего коэффициента корреляции
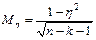 |
где k - число факторов КМ, включая результативный
| R | n | k | M | t | |
| 0, 7 | 0, 13 | 5, 32 | |||
| 0, 7 | 0, 15 | 4, 55 | |||
| 0, 7 | 0, 19 | 3, 63 | |||
| 0, 7 | 0, 29 | 2, 38 |
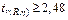
Для простого расчета
Коэффициент детерминации определяет на сколько процентов учтенные в корреляционной модели факторы объясняют изменение результативного показателя
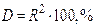 |
Для простого расчета
Модель устойчива, если D> 70%
Следовательно если R> =0, 83 то модель устойчива
Общую оценку адекватности (правдивости) уравнения дает критерий Фишера
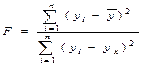 | 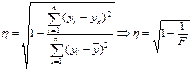 | ||
Как определить F численно?
Полученное значение критерия (Fрасч.) сравнивают с критическим (табличным) (Fтабл.) для принятого уровня значимости (a = 0, 05 или a = 0, 01 и числа степеней свободы (n 1 = m – 1 и n 2 = n – m, где n – число наблюдений, m – число факторов уравнения, включая результативный). Если оно окажется больше соответствующего табличного значения, то данное уравнение статистически значимо, т. е. доля вариации, обусловленная регрессией намного превышает случайную ошибку.
Таким образом проверенную модель можно использовать в практических целях
Еxcel дает возможность срезу получить все характеристики
***
Оценка параметров это только этап длительного и сложного процесса построения эконометрической модели. Первый результат очень редко является удовлетворительным во всех отношениях. Обычно приходится постепенно подбирать как формулу связи, так и состав объясняющих переменных, анализируя на каждом этапе качество оцененной зависимости. Этот анализ качества включает статистическую и содержательную составляющую. Проверка статистического качества оцененного уравнения состоит из следующих элементов:
· проверка статистической значимости каждого коэффициента уравнения регрессии;
· проверка общего качества уравнения регрессии;
· проверка свойств данных, выполнение которых предполагалось при оценивании уравнения.
Под содержательной составляющей анализа качества понимается рассмотрение экономического смысла оцененного уравнения регрессии: действительно ли значимыми оказались объясняющие факторы, важные с точки зрения теории; положительны или отрицательны коэффициенты, показывающие направление воздействия этих факторов; попали ли оценки коэффициентов регрессии в предполагаемые из теоретических соображений интервалы.
При анализе естественно сравнить фактические значения переменных с их прогнозными значениями YПронозн, чтобы оценить возможные погрешности предсказания зависимой переменной. Такой анализ называют анализом остатков.
Коэффициент корреляции Пирсона между известными значениями зависимой переменной и ее оценками это один из способов получения коэффициента множественной корреляции (КМК). Этот коэффициент выражает степень линейной связи одной переменной с множеством других и может изменяться от 0 до 1 вместе с ростом качества модели множественной регрессии.
Квадрат этого коэффициента есть доля дисперсии зависимой переменной. Он обусловлен влиянием всех независимых переменных.
Следует отметить, что соотношение величин коэффициентов регрессии, как правило, не позволяет судить о воздействии того или иного фактора на зависимую переменную, так как зависимые переменные измеряются обычно в разных шкалах и имеют разный масштаб. Поэтому вычисления, необходимые для множественного регрессионного анализа,
обычно начинаются с преобразования первичных данных (зависимой и независимых переменных) к z-значениям. Тогда уравнение регрессии принимает вид:

где β i – стандартные коэффициенты регрессии (β – коэффициенты).
Для частного случая одной независимой переменной стандартный коэффициент регрессии совпадает с коэффициентом корреляции данной независимой и зависимой переменных. Но при двух и более независимых переменных абсолютная величина коэффициента β i зависит не только от корреляции данной независимой и зависимой переменных, но и от корреляций этой независимой переменной с другими переменными. Только при условии отсутствия таких корреляций коэффициент β i для независимой переменной будет равен ее корреляции с зависимой переменной.
Абсолютная величина коэффициента β i характеризует относительное влияние независимой переменной (с учетом влияния других независимых переменных) на прогнозируемое значение зависимой переменной. Произведение β j riY, где riY – коэффициент корреляции данной независимой и зависимой переменных – это вклад i -ой переменной в дисперсию зависимой переменной.
Часть дисперсии зависимой переменной, которая обусловлена совокупным влиянием всех независимых переменных, называется коэффициентом множественной детерминации (КМД), который равен квадрату коэффициента множественной корреляции (КМК).
Таким образом, коэффициент множественной корреляции, определяющий состоятельность модели (общепринятое обозначение R) можно вычислить не только как корреляцию прогнозируемого и фактического значений зависимой переменной, но и по формуле:

Обычно для анализа общего качества оцененной линейной регрессии используют квадрат коэффициента множественной корреляции (КМК). Для случая парной регрессии это квадрат коэффициента корреляции переменных х и у. Коэффициент множественной детерминации (КМД) рассчитывается по формуле:
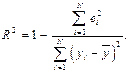
Он характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения. В качестве меры разброса зависимой переменной обычно используется ее дисперсия, а остаточная вариация может быть измерена как дисперсия отклонений вокруг линии регрессии. Если числитель и знаменатель вычитаемой из единицы дроби разделить на число наблюдений N, то получим, соответственно, оценки остаточной дисперсии и дисперсии зависимой переменной у. Отношение остаточной и общей дисперсий представляет собой долю необъясненной дисперсии. Если же эту долю вычесть из единицы, то получим долю дисперсии зависимой переменной, объясненной с помощью регрессии.
Чтобы получить несмещенные оценки (существенно при малом числе данных), делается поправка на число степеней свободы; тогда
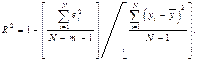
Для парной регрессии число независимых переменных т равно 1,
В числителе дроби, которая вычитается из единицы, стоит сумма квадратов отклонений наблюдений от линии регрессии, в знаменателе - от среднего значения переменной у. Таким образом, дробь эта мала (а коэффициент R 2 близок к единице), если разброс точек вокруг линии регрессии значительно меньше, чем вокруг среднего значения. По сути МНК позволяет найти прямую, для которой сумма квадратов ошибок прогноза минимальна, по отношению к аналогичной оценке, выполненной дляпрогноза только по среднему значению. Иначе говоря, коэффициент детерминации R2 показывает, в какой степени найденная регрессионная прямая дает лучший результат для объяснения поведения зависимой переменной у, чем просто горизонтальная прямая 
Смысл коэффициента детерминации может быть пояснен и немного иначе. Можно показать, что
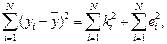
где ki – отклонение i -й точки на линии регрессии от 
Величину в левой части можно интерпретировать как меру общего разброса (вариации) переменной y, первое слагаемое в правой части – разброс, объясняемый с помощью регрессии, второе слагаемое – разброс, необъясненный с помощью регрессии. Следовательно, если две объясняющие переменные сильно коррелируют между собой, то они объясняют одну и ту же часть разброса переменной у, и в этом случае трудно идентифицировать вклад каждой из переменных в объяснение поведения у, значит одну из них желательно исключить из рассмотрения.
Если существует статистически значимая линейная связь, токоэффициент R2 близок к единице. Но он может быть близким к единице просто в силу того, что обе эти величины имеют выраженный временной тренд, не связанный с их причинно-следственной взаимозависимостью. В экономике обычно объемные показатели (доход, потребление, инвестиции) имеют такой тренд. Поэтому при оценивании линейных регрессий по временным рядам объемных показателей (например, зависимости выпуска от затрат ресурсов или объема потребления от величины дохода) величина R2 обычно очень близка к единице. Это говорит о том, что зависимую переменную нельзя описать просто как равную своему среднему значению, что заранее очевидно, раз она имеет временной тренд.
Точную границу приемлемости показателя R2 указать сразу для всех случаев невозможно. Нужно принимать во внимание и число степеней свободы уравнения, и наличие трендов переменных, и содержательную интерпретацию уравнения.
Условия получения приемлемых результатов:
· Продуманность исследования. Если нет смысловой связи между рассматриваемыми величинами, то результаты будут бесполезными.
· Чем больше переменных, тем больше нужна выборка. Обоснованных границ нет, но если наблюдений менее 50, то обычно возникают проблемы со значимостью.
· Данные не должны содержать ошибок.
· Желательна, но не обязательна близость всех распределений к нормальному распределению.
· Крайне нежелательно использовать независимые переменные, коэффициент корреляции между которыми по модулю близок к единице. Вообще с ростом линейных зависимостей между переменными надежность результатов снижается.