Проверка выполнимости предпосылок МНК. Статистика Дарбина–Уотсона

Статистическая значимость коэффициентов регрессии и близкое к единице значение коэффициента детерминации R ² еще не гарантируют высокого качества уравнения регрессии. Оценивая линейное уравнение регрессии, мы предполагаем, что реальная взаимосвязь переменных линейна, а отклонения от регрессионной прямой

являются случайными, независимыми друг от друга величинами с нулевым математическим ожиданием и постоянной дисперсией. Если эти предположения не выполняются, то оценки коэффициентов регрессии не обладают свойствами несмещенности, эффективности и состоятельности, и анализ их значимости будет неточным.

Причинами, по которым отклонения не обладают перечисленными выше свойствами, могут быть либо нелинейный характер зависимости между рассматриваемыми переменными, либо наличие неучтенного в уравнении существенного фактора. Действительно, при нелинейной зависимости между переменными отклонения от прямой регрессии не случайно распределены вокруг нее, а обладают определенными закономерностями, которые зачастую выражаются в существенном преобладании числа пар соседних отклонений с совпадающими знаками над числом пар с противоположными знаками. Отсутствие в уравнении регрессии какого-либо существенного фактора может также служить причиной устойчивых отклонений зависимой переменной от линии регрессии в ту или иную сторону. Добиться выполнимости предпосылок МНК в этих ситуациях можно либо путем использования какой-то другой нелинейной формулы, либо включением в уравнение регрессии новой объясняющей переменной. Это позволит реалистичнее отразить поведение зависимой переменной.

При статистическом анализе уравнения регрессии на начальном этапе чаще других проверяют выполнимость одной предпосылки, а именно, условия статистической независимости отклонений между собой. При этом обычно проверяется их некоррелированность, являющаяся необходимым, но недостаточным условием независимости. Причем проверяется некоррелированность не любых, а только соседних величин e _i. Соседними обычно считаются отклонения соседние по возрастанию объясняющей переменной x (при рассмотрении временных рядов по времени). Для этих величин рассчитывают коэффициент корреляции, называемый в этом случае коэффициентом автокорреляции первого порядка.

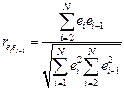
При этом учитывается, что математическое ожидание отклонений равно нулю.

На практике вместо коэффициента автокорреляциииспользуют статистику Дарбина-Уотсона DW, рассчитываемую по более простой формуле:

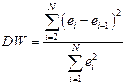
Очевидно, что при больших N выполняется соотношение: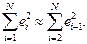

Тогда легко вывести зависимость:

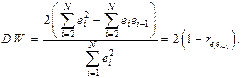
Суть статистики Дарбина-Уотсона DW можно осмыслить следующим образом. Если каждое следующее отклонение приблизительно равно предыдущему, то каждое слагаемое в числителе дроби последней формулы близко нулю и, следовательно, статистика DW окажется близкой к нулю. В этом случае коэффициент автокорреляциидолжен

быть близок к единице, что будет подтверждать наличие положительной автокорреляции остатков первого порядка (линейной зависимости между остатками).

Если же точки наблюдений поочередно отклоняются в разные стороны от линии регрессии то:

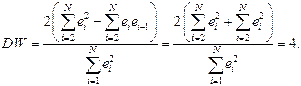
Это случай отрицательной автокорреляции остатков первого порядка.

При случайном поведении отклонений можно предположить, что в одной половине случаев знаки последовательных отклонений совпадают, а в другой - противоположны. Так как абсолютные величины отклонений в среднем предполагаются равными, то можно считать, что в половине случаев они равны, а в другой равны по абсолютной величине, но противоположны по знаку. Тогда

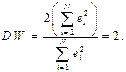
В этом случае коэффициент автокорреляции должен быть нулевым. Таким образом, необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина-Уотсона.

Тогда, если DW ≈ 2, мы считаем отклонения от регрессии случайными (хотя они в действительности могут и не быть таковыми). Это означает, что построенная линейная регрессия, вероятно, отражает реальную зависимость. Скорее всего, не осталось неучтенных существенных факторов, влияющих на зависимую переменную. Какая-либо другая нелинейная формула не превосходит по статистическим характеристикам предложенную линейную зависимость. В этом случае, даже когда R ² невелико, вполне вероятно, что необъясненная дисперсия вызвана влиянием на зависимую переменную большого числа различных факторов, индивидуально слабо влияющих на исследуемую переменную, и может быть описана как случайная нормальная ошибка.

Чтобы ответить на вопрос, какие значения DW можно считать статистически близкими к двум есть готовые таблицы критических точек статистики Дарбина-Уотсона, позволяющие при данном числе наблюдений N, количестве объясняющих переменных m и заданном уровне значимости (обычно 0, 05) определять критические точки, что можно иллюстрировать следующим рисунком.

Не обращаясь к таблице критических точек Дарбина-Уотсона, можно пользоваться " грубым" правилом и считать, что автокорреля

ция остатков отсутствует, если 1, 5 < DW < 2, 5.

Конечно, статистический анализ построенной регрессии является достаточно сложным и многоступенчатым процессом, имеющим определенную специфику в каждом конкретном случае. Однако базовыми пунктами такого анализа, отраженными во всех эконометрических

пакетах, являются проверка статистической значимости коэффициентов регрессии и коэффициента детерминации, анализ статистики Дарбина-Уотсона.