Тесты на наличие автокорреляции

Статистика Дарбина—Уотсона, безусловно, является наибо­лее важным индикатором наличия автокорреляции. Однако, как уже отмечалось, тест обладает и определенными недостатками. Это и наличие зоны неопределенности, и ограниченность результата (выявляется лишь корреляция между соседними членами). Ничего нельзя сказать и о характере автокорреляции.

Это приводит к необходимости использовать также и другие тесты на наличие автокорреляции. Во всех этих тестах в качестве основной гипотезы фигурирует гипотеза об отсутствии автокорреляции.

Рассмотрим две наиболее часто встречающиеся причины коррелированности регрессоров и ошибок регрессии.

1. На случайный член ε воздействуют те же факторы, что и на формирование значений регрессоров.

Рассмотрим следующий модельный пример.

В поселке А производится сырье двух видов I и II. Сырье перевозится в город В, где на заводе производится субпродукт, который продается фирме-производителю по цене X. Фирма изготовляет из субпродукта конечный товар, который перевозится в областной центр и реализуется по цене Y Цены на сырье первого и второго типа меняются и образуют временные ряды Z ₁и Z ₂

Допустим, фирма-производитель хочет построить зависимость цены реализации Y от цены X и рассматривает регрессионную модель .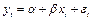

Насколько достоверны полученные результаты? Очевидно, и доставка сырья в город В, и доставка конечного продукта в город С связаны с перевозками, а значит, такие факторы, как затраты на топливо, зарплата водителей, состояние дорог и т. д. будут влиять и на формирование цены X, и на конечную цену Y при заданном X, т. е. на величину ошибок регрессии модели. Таким образом, регрессоры и ошибки регрессии оказываются коррелированными, и оценки, полученные методом наименьших квадратов, несостоятельны.

В следующем параграфе мы вернемся к этому модельному примеру, а пока отметим вторую типичную причину коррелированности объясняющих переменных и случайного члена.

2. Ошибки при измерении регрессоров. Пусть при измерении регрессора X _j допускается случайная ошибка, следовательно, в фактически рассматри­ваемой модели имеется корреляция между фиксируемыми значениями регрессоров и случайным членом.

Отметим, что обе указанные причины коррелированности регрессоров и ошибок регрессии имеют один и тот же математический смысл; значения объясняемых переменных формируются не присутствующим в модели регрессором, а каким-то другим, и, стало быть, оценивается «не тот» параметр.

При рассмотрении конкретных регрессионных моделей временных рядов с коррелированностью регрессоров и ошибок приходится сталкиваться довольно часто. Наиболее часто используемый прием, применяемый в подобных случаях, — метод инструментальных переменных. Идея метода заключается в том, чтобы подобрать новые переменные Z _j (j = 1,..., e), которые бы тесно коррелировали с X _j и не коррелировали с ошибками. Этот набор переменных может включать те регрессоры, которые не коррелируют с ε, а также другие величины. При этом, вообще говоря, количество новых переменных может отличаться от исходного количества регрессоров (обычно в большую сторону). Такие переменные Z _i,..., Z _e называются инструментальными. Они позволяют построить состоятельную оценку параметра β модели.