Методы смягчения проблемы гетероскедастичности

Гетероскедастичность приводит к неэффективности оценок, несмотря на их несмещенность. Это может привести к необоснованным выводам по качеству модели. Поэтому при установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии отклонений.

При известных для каждого наблюдения значениях дисперсии можно устранить гетероскедастичность, разделив каждую из пар наблюдений на известную величину среднеквадратической ошибки.Наблюдениям с наименьшими дисперсиями придаются наибольшие " веса", а с максимальными дисперсиями - наименьшие " веса". Действительно, наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке коэффициентов регрессии, чем наблюдения с большими дисперсиями. Учет этого факта увеличивает вероятность получения более точных оценок.

На практике фактические значения дисперсий отклонений известны крайне редко. Следовательно, чтобы применить метод взвешенных наименьших квадратов, необходимо сделать реалистические предположения о значениях дисперсий отклонений.

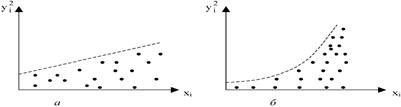
Дисперсии пропорциональны х _i, (рис. а) .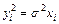

Дисперсии пропорциональны 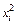, (рис. б) .

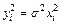Следовательно, преобразование уравнения регрессии сведется к делению на