Нелинейные модели регрессии

До сих пор мы рассматривали линейные регрессионные модели, в которых переменные имели первую степень (модели, линейные по переменным), а параметры выступали в виде коэффициентов при этих переменных (модели, линейные по параметрам). Однако соотношение между социально-экономическими явлениями и процессами далеко не всегда можно выразить линейными функциями, так как при этом могут возникать неоправданно большие ошибки.

Так, например, нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства — трудом, капиталом и т. п.), функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом) и другие.

Для оценки параметров нелинейных моделей используются два подхода.

1-й подход основан на линеаризации модели и заключатся в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.

2-й подход обычно применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных.

Для линеаризации модели в рамках первого подхода могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам.

Если модель нелинейна по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов.

Так, например, если нам необходимо оценить параметры регрессионной модели

,

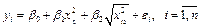то вводя новые переменные, 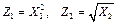, получим линейную модель 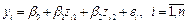, параметры которой находятся методом наименьших квадратов.

Более сложной проблемой является нелинейность модели по параметрам, так как непосредственное применение метода наименьших квадратов для их оценивания невозможно. К числу таких моделей можно отнести, например, мультипликативную {степенную) модель

,

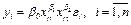экспоненциальную модель

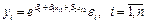
и другие.

В ряде случаев путем подходящих преобразований модели удается привести к линейной форме. Так, мультипликативную и экспоненциальную модели можно привести к линейной логарифмированием обеих частей уравнения.

Тогда можно применять обычные методы исследования линейной регрессии. Однако следует подчеркнуть, что критерии значимости и интервальные оценки параметров, применяемые для нормальной линейной регрессии, требуют, чтобы вектор возмущений имел логарифмически нормальное распределение.

Заметим, что модель

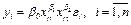нельзя привести к линейному виду. В этом случае используются специальные (итеративные) процедуры оценивания параметров.