
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Временные ряды и прогнозирование
|
|
При рассмотрении классической модели регрессии характер экспериментальных данных, как правило, не имеет принципиального значения. Методы исследования моделей, основанных на данных пространственных выборок и временных рядов, вообще говоря, существенно отличаются. Объясняется это тем, что в отличие от пространственных выборок наблюдения во временных рядах, как правило, нельзя считать независимыми.
Под временным рядом (динамическим рядом, или рядом динамики) в экономике подразумевается последовательность наблюдений некоторого признака (случайной величины) Y в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые будем обозначать y t (t = 1, 2,..., n), где n — число уровней.
В табл. – спрос на некоторый товар за 8-летний период (усл. ед), т. е. временной ряд спроса y t.
| Год, t | ||||||||
| Спрос, y t |
В качестве примера на рис. временной ряд y t изображен графически.
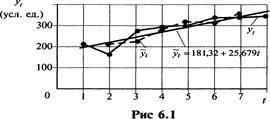
В общем виде при исследовании экономического временного ряда y t выделяются несколько составляющих:
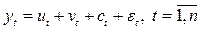 ,
,
где u t — тренд, плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов, т. е. длительную («вековую») тенденцию изменения признака (например, рост населения, экономическое развитие, изменение структуры потребления и т. п.);
v t — сезонная компонента, отражающая повторяемость экономических процессов в течение не очень длительного периода (года, иногда месяца, недели и т. д., например, объем продаж товаров или перевозок пассажиров в различные времена года);
ct — циклическая компонента, отражающая повторяемость экономических процессов в течение длительных периодов (наример, влияние волн экономической активности Кондратьева, демографических «ям», циклов солнечной активности и т. п.);
ε t — случайная компонента, отражающая влияние не поддающихся учету и регистрации случайных факторов.
Следует обратить внимание на то, что в отличие от ε tпервые три составляющие (компоненты) являются закономерными, неслучайными.
Важнейшей классической задачей при исследовании экономических временных рядов является выявление и статистическая оценка основной тенденции развития изучаемого процесса и отклонений от нее.
Отметим основные этапы анализа временных рядов:
· графическое представление и описание поведения временного ряда;
· выделение и удаление закономерных (неслучайных) составляющих временного рада (тренда, сезонных и циклических составляющих);
· сглаживание и фильтрация (удаление низко- или высокочастотных составляющих временного ряда);
· исследование случайной составляющей временного ряда, построение и проверка адекватности математической модели для ее описания;
· прогнозирование развития изучаемого процесса на основе имеющегося временного ряда;
· исследование взаимосвязи между различными временными рядами.
Среди наиболее распространенных методов анализа временных рядов выделим корреляционный и спектральный анализ, модели авторегрессии и скользящей средней.
В отличие от элементов случайной выборки члены временного ряда, как правило, не являются статистически независимыми. Во-вторых, члены временного ряда не являются одинаково распределенными.
Одна из важнейших задач анализа временного ряда состоит в прогнозировании на его основе развития изучаемого процесса. При этом исходят из того, что тенденция развития, установленная в прошлом, может быть распространена (экстраполирована) на будущий период. Задача ставится так: имеется временной (динамический) ряд yt (t = l, 2,..., n) и требуется дать прогноз уровня этого ряда на момент n +τ.
Прогноз развития изучаемого процесса на основе экстраполяции временных рядов может оказаться эффективным, как правило, в рамках краткосрочного, в крайнем случае, среднесрочного периода прогнозирования.