
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Одноэтапная и двухэтапная схемы корреляционного анализа, каскадный эконометрический анализ
|
|
1. Анализ использования ресурсного потенциала предприятия
2. Корреляционные модели при анализе региональной экономики
3. Каскадный эконометрический анализ
- Анализ использования ресурсного потенциала предприятия
Как известно эконометрические модели используются для целей анализа и прогноза. Разберем подробно вопросы связанные с анализом экономических показателей. С точки зрения рыночной экономики успешные предприятия это те, которые наиболее эффективно используют имеющиеся ресурсы и ресурсный потенциал.
Допустим, что имеется корреляционная модель формирования урожайности зерновых:
yx = 4, 2 + 0, 3 x 1 + 6, 0 x 2.
где: X1– плодородие пашни, баллы
X2 –внесение минеральных удобрений, ц. д. в-ва на 1 га посева зерновых
В полученной модели tR, r, η > 2, 48, taj > 1, 96, F 1 > 1, 5. В этом случае наша модель может быть использована для целей анализа и планирования показателей.
Первым этапом анализа на базе корреляционной модели является сравнение расчетных и фактических значений результативного показателя.
Чтобы получить расчетные значения ух, в корреляционную модель подставляем фактические значения факторов.
При этом в трех предприятиях фактическая (yi) и расчетная (yx) урожайности зерновых составляют:
в хозяйстве № 1 — yx = 28, yi = 28;
в хозяйстве № 2 — yx = 23, yi = 24;
в хозяйстве № 3 — yx = 31, yi = 30.
При традиционной оценке эффективности использования ресурсов лучшим считалось бы третье хозяйство с большей по абсолютной величине урожайностью зерновых. Если же анализ эффективности использования ресурсов проводился с помощью корреляционной модели, то в этом случае мы учли бы то, при каких условиях и расходовании ресурсов была получена соответствующая урожайность.
Анализ показывает, что при факторных значениях х 1, x 2 и среднем уровне хозяйствования первое хозяйство должно было получить столько зерна, сколько было получено фактически, второе — меньше фактического, третье — больше. В данном случае (с точки зрения эффективности использования ресурсов) лучше других работало второе хозяйство.
Таким образом, приведенный пример свидетельствует о том, что корреляционная модель является аппаратом объективной оценки эффективности использования ресурсов или формирования показателей. На основе корреляционной модели можно выявить устойчивые тенденции в экономике и те параметры (лучшие), при которых ресурсы используются наиболее эффективно.
Чтобы выявить закономерности и лучшие параметры в экономике, построим на основе корреляционной модели группировку
по следующей методике:
1. Рассчитываем параметры корреляционной модели.
2. Если в корреляционной модели tR, r, η , aj > min, то производим сравнение расчетных и фактических значений и выделяем предприятия (опыты), для которых характерны следующие ситуации:
yх > yi; 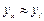 ; yx < yi.
; yx < yi.
По каждой из этих групп ситуаций рассчитываем среднее значение факторов (х 1... хn), учтенных в корреляционной модели. При этом также можем рассчитать средние значения других факторов.
3. Сравнивая средние значения факторов указанных грех групп, выясняем то, как изменяются факторы в каждой из этих групп. При этом в лучшей группе имеются средние значения факторов, которые можем считать оптимальными и ориентирами для остальных групп.
В условиях нерыночной системы хозяйствования в качестве
базы для формирования цен брались средние по совокупности
издержки, т. е. издержки предприятий первой, второй, и третьей групп, хотя предприятия худшей по показателям труппы имели низкую окупаемость затрат, в том числе из-за низкого уровня хозяйствования и организации производства.
В рыночных условиях система хозяйствования не может ориентироваться на подобные предприятия, которые могут стать банкротами. Это означает, что в качестве издержек, на основе которых будут формироваться цены, принимаются издержки предприятий лучшей и средней по показателям групп.
В этой связи необходимо обосновывать показатели лучших
и средних по эффективности использования ресурсов групп хозяйств, показатели которых будут являться ориентиром в развитии экономики, основой при формировании цен на продукцию. Решать эти задачи позволяют корреляционные модели. При этом наиболее приемлемой является двухэтапная схема корреляционного анализа.
2. Корреляционные модели при анализе региональной экономики
Цель анализа — выяснить устойчивые тенденции развития экономики большой группы предприятий, расположенных на значительной территории. Методика анализа включает следующие этапы:
1. Выделяется показатель, который может быть обобщающим с точки зрения эффективности использования ресурсов (например, прибыль и др.).
2. Определяются факторы, формирующие результативный показатель.
3. Выделяются территории со схожими природно-климатиче-
скими и экономическими условиями (в пределах региона).
4. Строится корреляционную модель формирования результативного показателя по предприятиям выделенных территорий
(округов).
5. На основе сравнения расчетных и фактических значений результативного показателя в каждом округе выделяют 3 группы хозяйств
(с лучшими, средними и худшими условиями хозяйствования)
или 2 группы (если выделяют группы хозяйств только с лучшими
и худшими условиями).
По информации каждой из групп (территорий каждого из округов) строят корреляционную модель формирования результативного показателя. При этом учитывается требование, что число
хозяйств (или опытов) должно быть не меньше 20 или больше 2, 5 k, где k — число факторов (включая результативный).
Сравнивая коэффициенты регрессии при одноименных факторах и выясняя различия в окупаемости ресурсов, делаем предположение о том, где лучше реализовать ограниченные ресурсы с тем, чтобы общий эффект был больше.
Данная методика использовалась для анализа окупаемости
ресурсов сельскохозяйственных организаций Могилевской области.
В области было выделено 2 округа: Северо-Восточный и Восточный (Хотимский, Костюковичский, Климовичский районы, частично Кричевский). Были рассчитаны корреляционные модели формирования стоимости товарной продукции (ТП) в разрезе округов (таблица 13.2).
Данные свидетельствуют о том, что предприятия округов существенно отличаются окупаемостью практически всех (за исключением энергетических мощностей) ресурсов.
В таблице 13.2 приведены коэффициенты регрессии при факторах по предприятиям обоих округов. Абсолютные значения коэффициентов регрессии и знаки при них свидетельствуют о значении отдельных факторов. Так, увеличение численности среднегодовых работников в хозяйствах Северо-Восточного округа не приводит к положительному эффекту, в то время как в Восточном округе с ростом численности работников стоимость товарной продукции возрастает.
Таблица 13.2 — Тенденции развития и параметры окупаемости
ресурсов сельскохозяйственных организаций Могилевской области
| Уровень использования ресурсного потенциала | Стоимость ТП (тыс. у. е.) на единицу ресурсного потенциала | |||||||
| Среднегодовые работники, чел. | Основные производственные фонды, тыс. у. е. | Производствен-ные затраты, без амортизации, тыс. ед. | Энергетические мощности, л. с. | Покупные комбикорма, тыс. у. е. | Покупной скот, тыс. у. е. | Сотни баллогек- таров, баллы/га | ||
| Северо-вос- точный округ | Средний (для всех хозяйств) | -0, 709 | 0, 143 | 0, 602 | 0, 028 | 1, 070 | -0, 02 | 0, 380 |
| Выше среднего | -1, 662 | 0, 142 | 0, 694 | 0, 038 | 0, 702 | 0, 286 | 0, 834 | |
| Ниже среднего | 0, 521 | 0, 147 | 0, 336 | 0, 027 | 1, 755 | -0, 195 | 0, 333 | |
| Восточный округ | Средний (для всех хозяйств) | 0, 582 | 0, 060 | 0, 101 | 0, 019 | 2, 064 | 1, 280 | 0, 762 |
| Выше среднего | 0, 232 | 0, 070 | 0, 370 | 0, 014 | 2, 301 | 1, 460 | 0, 704 | |
| Ниже среднего | 1, 027 | 0, 053 | 0, 077 | 0, 047 | 1, 094 | 0, 764 | 0, 715 |
Отсюда можно сделать вывод, что в отличие от большинства
хозяйств Северо-Восточного округа во всех хозяйствах Восточного округа наметился дефицит трудовых ресурсов.
Поскольку в рамках каждого из округов имеются сельскохозяйственные организации с различным уровнем использования ресурсов, то были выделены две группы таких хозяйств (с лучшим и худшим уровнями использования ресурсов). В разрезе этих групп были рассчитаны параметры той же корреляционной модели и получены коэффициенты регрессии, которые объясняют эффективность ресурсов в разрезе выделенных групп и округов. В результате этого было выяснено то, что средняя эффективность отдельных факторов по округам существенно отличается (если рассматривать ее в разрезе хозяйств с эффективностью использования ресурсов выше и ниже среднего уровня). Так, в хозяйствах Северо-восточного округа с эффективностью производства ниже среднего уровня имеет место дефицит трудовых ресурсов и, следовательно, увеличение численности работающих в этих хозяйствах предполагает увеличение стоимости товарной продукции. Значительно отличаются от средних по округу коэффициенты регрессии и при других факторах.
Таким образом, анализируя данные таблицы 13.2, можно отметить следующее: чем выше значение коэффициента регрессии, тем больше наблюдается недостаток ресурса. Следовательно, необходимо направлять ресурсы именно в те хозяйства, где этих ресурсов не хватает. Например, покупку комбикормов целесообразнее всего осуществлять в лучших хозяйствах Восточного округа (а = 2, 301)
и худших хозяйствах Северо-Восточного округа (а = 1, 755).