Каскадный эконометрический анализ

Мультиколлинеарность это сильная линейная взаимосвязь двух или нескольких факторных переменных. из вышесказанного следует, что мультиколлинеарность может возникнуть при построении множественных линейных регрессионных моделей.

В том случае, если факторные переменные связаны между собой функциональной зависимостью, то говорят о наличии совершенной мультиколлинеарности.

Пусть имеется информация об уровне рентабельности зерна, урожайности зерновых культур и дозах внесения минеральных удобрений.

Таблица 21 – Показатели производства и реализации зерна

Несложный логический анализ показывает, что на уровень рентабельности оказывают влияние и урожайность, и дозы внесения удобрений. Следовательно, в будущей эконометрической модели уровень рентабельности будет результативным показателем (Y). Соответственно, урожайность зерновых (X₁) и доза внесения удобрений (X₂) – это факторные признаки.

С помощью программы ”Регрессия” было получено следующее уравнение:

Y = -15, 4 + 0∙ X₁ + 0, 29∙ X₂, R = 0, 93.

Согласно уравнению регрессии, урожайность зерновых не оказывает абсолютно никакого влияния на уровень рентабельности зерна. Дело в том, что между факторными переменными X₁ и X₂ существует строгая функциональная зависимость. В самом деле, для любого опыта значение фактора X₂ в 4 раза превышает соответствующее значение признака X₁. Можно записать, что X₂ = 4 X₁. В этом случае коэффициент парной корреляции между факторными признаками r_x1x2 будет равен единице.

Совершенная мультиколлинеарность крайне редко встречается на практике. Значительно чаще мы сталкиваемся с несовершенной мультиколлинеарностью, когда между факторными переменными существует тесная корреляционная зависимость.

Мультиколлинеарность не позволяет объективно оценить влияние факторных признаков на результативную переменную. Как следствие этого, коэффициенты регрессии и их статистические оценки не будут являться надежными. В некоторых случаях возможно даже получение неверного знака у того или иного коэффициента регрессии. Все это снижает качество эконометрической модели в целом.

Сущность мультиколлинеарности можно наглядно показать с помощью.. физического опыта. Предположим, что три человека A, B и С соединены канатом (рисунок 12).

Человек A является физически более сильным, чем остальные участники и он условно будет отражать результативный показатель. Оппонентами сильнейшего участника будут два человека: B и C. Слабейшие участники будут стремиться вдвоем выиграть перетягивание каната у игрока A. Пусть при первом испытании участники: B и C не станут сражаться с человеком A, а свои усилия направят друг против друга. В этом случае, силач A, применив даже небольшую силу, сможет без труда выиграть соревнование по перетягиванию каната. Однако, если слабейшие игроки не станут выяснять отношения между собой, а будут действовать сообща против их соперника, то у участников B и C появятся все шансы, чтобы выиграть соревнование.

Усиление зависимости между факторами (в последнем примере B и C условно считаются факторами) ведет к ослаблению влияния данных факторов на результат.

Наличие мультиколлинеарности может быть выявлено на основании нескольких признаков.

1. Коэффициент множественной корреляции R достаточно высок, но отдельные коэффициенты регрессии имеют низкие характеристики.

2. Коэффициент парной корреляции между двумя факторными признаками будет находиться на достаточно высоком уровне.

3. Высокие частные коэффициенты корреляции. Их целесообразно рассчитывать в тех случаях, когда число факторов эконометрической модели больше двух. Частные коэффициенты корреляции характеризуют силу линейной зависимости между двумя признаками без учета влияния на них других факторов. Например, если в уравнении регрессии используются 3 независимые (факторные) переменные X₁, X₂ и X₃, то частный коэффициент корреляции между X₁ и X₂ рассчитывается по формуле:

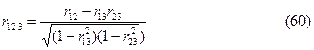
Предположим, что получены следующие коэффициенты парной корреляции: r₁₂ = 0, 6; r₁₃ = 0, 4; r₂₃ = -0, 4.

Рассчитаем частный коэффициент корреляции:

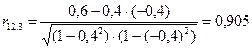
Полученный коэффициент r_12.3 = 0, 905 указывает на высокую зависимость (иначе говоря коллинеарность) между переменными X₁ и X₂. Вместе с тем, ”обычный” коэффициент парной корреляции r₁₂ =0, 6 и свидетельствует лишь о средней силе связи между изучаемыми факторами. В силу мультиколлинеарности коэффициенты регрессии отдельных факторов могут быть значительно завышены или занижены.

Чтобы избежать искажения коэффициентов регрессии в корреляционной модели с мультиколлинеарными факторами используется каскадный корреляционный анализ, сущность которого заключается в следующем:

1. Выбираем результативный и факторные показатели и проверяем информацию столбцов на достоверность.

2. Определяем пары тесно связанных друг с другом факторов,
т. е. коррелируемых (например, в корреляционной модели формирования стоимости валовой продукции такой парой факторов являются основные производственные и оборотные фонды).

3. Определяем, какие из факторов тесно связанных пар являются ведущими (определяющими). Эти определяющие факторы назовем промежуточными результативными.

4. Строим парную корреляционную модель взаимосвязи каждой пары факторов, например, 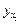= а ₀ + а ₁ х ₁, где 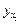— стоимость оборотных фондов; х ₁ — стоимость основных производственных фондов.

При этом рассчитываем все остальные характеристики (r, t_r, t_aj).

5. Рассчитаем разность фактических и расчетных значений фактора, тесно связанного с другим или другими факторами:

x₂ - 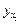= ∆ x₂.

В корреляционной модели вместо фактора х ₂ставим столбец Δ х ₂, определяющий величину отклонения фактического значения фактора от среднего уровня, и считаем параметры модели. В этом случае коэффициент регрессии при Δ х₂ определяет влияние на результативный показатель нового фактора при его отклонении от среднего уровня. При этом удается избежать искажения, которое имеет место в корреляционной модели с тесно коррелируемыми факторами.