Обнаружение гетероскедастичности

В ряде случаев на базе знаний характера данных появление проблемы гетероскедастичности можно предвидеть и попытаться устранить этот недостаток еще на этапе спецификации. Однако значительно чаще эту проблему приходится решать после построения уравнения регрессии.

Обнаружение гетероскедастичности в каждом конкретном случае является довольно сложной задачей, т. к. для знания дисперсий отклонений необходимо знать распределение СВ Y, соответствующее выбранному значению x _i СВ X. На практике зачастую для каждого конкретного значения х _i, определяется единственное значение y _i, что не позволяет оценить дисперсию СВ Y для данного x _i.

Естественно, не существует какого-либо однозначного метода определения гетероскедастичности. Однако к настоящему времени для такой проверки разработано довольно большое число тестов и критериев для них. Наиболее популярен и нагляден Графический анализ остатков. Использование графического представления отклонений позволяет определиться с наличием гетероскедастичности. В этом случае по оси абсцисс откладывается объясняющая переменная X (либо линейная комбинация объясняющих переменных), а по оси ординат либо отклонения либо их квадраты.

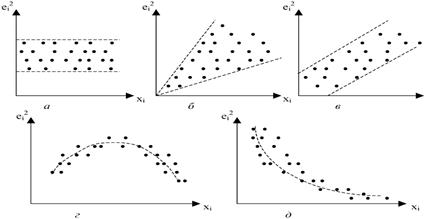
На рис. а все отклонения находятся внутри полуполосы постоянной ширины, параллельной оси абсцисс. Это говорит о независимости дисперсий от значений переменной X, т.е. в этом случае мы находимся в условиях гомоскедастичности.

Ситуации, представленные на рис. б - д, отражают большую вероятность наличия гетероскедастичности для рассматриваемых статистических данных.

Графический анализ отклонений является удобным и достаточно надежным в случае парной регрессии. При множественной регрессии графический анализ возможен для каждой из m объясняющих переменных отдельно. Чаще же вместо объясняющих переменных, по оси абсцисс откладывают прогнозируемые значения, получаемые из эмпирического уравнения регрессии.Такой анализ целесообразен при большом количестве объясняющих переменных.