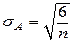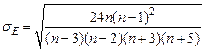Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Статистическая проверка гипотез в эконометрических исследованиях
|
|
1. Законы распределений случайных величин.
2. Генеральная совокупность и выборка.
3. Статистическая проверка гипотез.
1. Законы распределений случайных величин
Большинство СВ подчиняется тому или иному закону распределения, знание которого позволяет предвидеть вероятности попадания исследуемой СВ в определенные интервалы. Это необходимо чтобы осуществлять продуманную экономическую политику с учетом возможности возникновения той или иной ситуации. Очень часто реальные данные самой различной природы описываются нормальным законом распределения. Эта закономерность проявляется всегда, когда конечный результат определяется достаточно большим числом факторов, среди которых нет доминирующего. Тогда чем больше отклонение от средней величины, тем реже встречаемость таких отклонений при любых законах распределения отдельных факторов.
Предположим, монета подбрасывается 100 раз. И каждый раз она можете равным успехом выпасть «орлом» пли «решкой». Какова вероятность того, что в результате этой игры выпадет 0 «орлов», или 1 «орел»,..., 10 «орлов»? Де Муавру еще в XVIII веке удалось доказать, что при большом числе наблюдений уравнение кривой для любой подобной задачи описывается следующей формулой:

Отметим, что только два параметра: среднее значение и стандартное отклонение отличают друг от друга бесконечное множество нормальных кривых, одинаковой формы.
Среднее значение задает положение кривой на числовой оси, а стандартное отклонение определяет ширину этой кривой.
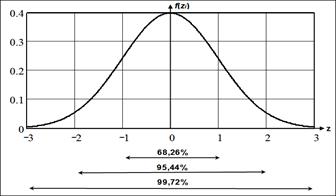
Получим единичное нормальное распределение, которое используется как стандарт — эталон. Его среднее значение 0 а стандартное отклонение 1. Его часто называют стандартным нормальным распределением. Кривая симметрична относительно Хср=0.
Приняв 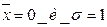 получим нормальное распределение.
получим нормальное распределение.
Площадь под кривой рaвнa 1, поэтому вероятность попадания СВ в заданный диапазон равна площади под кривой, лежащей между соответствующими точками, определяющими границы этого диапазона. Например, вероятность того, что отклонение от среднего значения не превысит удвоенного среднеквадратического отклонения составляет 95, 44%,
Наиболее часто встречаются значения признака, близкие к его среднему. По мере удаления от среднего значения число наблюдений или вероятность наступления события уменьшаются. Причем в интервал от - σ x до + σ x попадает 68, 3% случаев; от - 2 σ x до + 2 σ x – 95, 5%; от - 3 σ x до + 3 σ x – 99, 7% случаев. Поскольку в последний интервал попадает подавляющее большинство случаев при нормальном распределении, и называется иногда правилом «трех сигм».
Пример:
| № | ||||||||||
| Надой, ц | ||||||||||
| min | ||||||||||
| max | ||||||||||
| хср | ||||||||||
| σ x | 6, 3 | |||||||||
| Хср-3σ x | 17, 2 | |||||||||
| Хср+3σ x | 54, 8 |
Чтобы оценить степень отклонения графика распределения частот от симметричного вида относительно среднего значения используется такой показатель как асимметрия, который вычисляется по формуле:
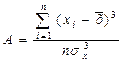 |
Распределение с положительной ассиметрией
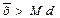 |
Распределение с отрицательной ассиметрией
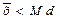 |
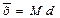 Симметричное распределение
Симметричное распределение
Для симметричного распределения асимметрия равна 0. Если чаще встречаются значения меньше среднего, то говорят о левосторонней, или положительной асимметрии (As> 0). Если же чаше встречаются значения больше среднего, то асимметрия – правосторонняя, или отрицательная (As< 0). Чем больше отклонение от нуля, тем больше асимметрия.
Для характеристики степени плосковершинности или остроконечности графика распределения служит показатель эксцесса, который определяется формулой:
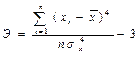 |
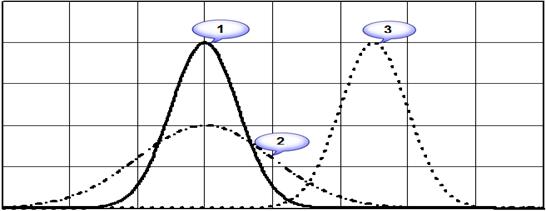
Вид распределения частот при разных значениях асимметрии и эксцесса показан на рисунке.
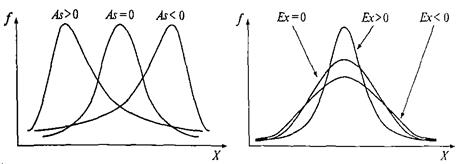
Для нормального распределения и асимметрия и эксцесс равны нулю.
| Распределение принимают | 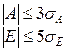
| |||||
| за нормальное, если выполняются | ||||||
| следующие неравенства: | ||||||
| где | ||||||
| ||||||
| стандартная ошибка ассиметрии | ||||||
| стандартная ошибка эксцесса | ||||||
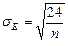
| ||||||
Упрощенно можно принять:
Для предварительной оценки характера распределения можно использовать графический способ (построить гистограмму). Правило 3сигма. А и Э.
При моделировании экономических процессов используются СВ, которые представляют собой алгебраическую комбинацию нескольких СВ. Для прогноза поведения таких СВ часто используется χ 2 - распределение и распределение Cтьюдента.
χ 2 - распределение получается при суммировании квадратов n СВ, имеющих стандартное нормальное распределение. Между этими СВ могут быть m линейных зависимостей. Оказывается, что величина υ = n-m, которую называют числом степеней свободы, полностью определяет характер распределения. Его график лежит в первой четверти декартовой системы координат и имеет асимметричный вид с вытянутым правым " хвостом". С увеличением числа степеней свободы распределение χ 2 постепенно приближается к нормальному. Его основные числовые характеристики: среднее M (χ 2) = υ, дисперсия D (χ 2) = 2 υ.
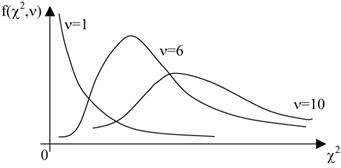
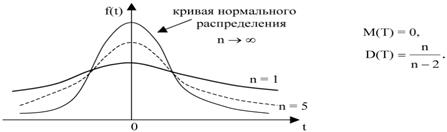
Распределение Cтьюдента (t -распределение) с числом степеней свободы n определяется как:
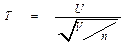
Где U имеет стандартное нормальное распределение, а V– независимая СВ распределенная по закону χ 2 с n степенями свободы. Этот параметр полностью определяет характер распределения. При n > 30 распределение Cтьюдента практически совпадает с нормальным.
2. Генеральная совокупность и выборка
Часто требуется определить некоторую количественную характеристику большой группы однородных объектов. Например, доход населения, количество покупателей в магазине в течение дня, процент брака в исследуемой партии и т. д. Такая объемлющая группа называется в статистике генеральной совокупностью. Теоретически считается, что объем генеральной совокупности не ограничен. Практически же объем генеральной совокупности всегда ограничен и может быть различным в зависимости от предмета наблюдения и решаемой задачи.
Выборкой называют часть генеральной совокупности, отобранную для изучения. Изучение всей генеральной совокупности почти всегда либо невозможно, либо нецелесообразно. Например, анализ среднего дохода населения г. Минска формально предполагает наличие достоверной информации о каждом жителе города в конкретный момент времени, что нереально. Но информация о генеральной совокупности, полученная на основании выборочного наблюдения, всегда будет иметь некоторую погрешность. Вряд ли средний доход, полученных по выборке объемом даже 1000 респондентов будет в точности таким же, что и во всем городе. Очевидно, что результат будет сильно зависеть и от метода отбора респондентов.
Поэтому требования, предъявляемые к любой выборке, сводятся к тому, что на ее основе должна быть получена наиболее полная, неискаженная информация об особенностях генеральной совокупности, из которой взята эта выборка. Если выборка представляет собой меньшую по размеру, но точную модель той генеральной совокупности, которую она должна отражать, то ее называют репрезентативной. Есть два метода, обеспечивающие репрезентативность выборки.
Первый метод – формирование простой случайной выборки. Элементы, отбираются из генеральной совокупности так, чтобы каждый элемент этой совокупности имел бы равную вероятность попасть в выборку. Получить простую случайную выборку можно путем обычной жеребьевки (по аналогии с лотереей) или с использованием случайных чисел. Но данная процедура требует учитывать каждого представителя генеральной совокупности, что не всегда возможно.
Второй метод предполагает, что элементы генеральной совокупности разбивают на страты (группы) в соответствии с некоторыми характеристиками. Например, при обследовании спроса на определенный товар генеральную совокупность желательно разбить на группы, различающиеся по величине дохода, социальной принадлежности, месту жительства и т.д. Тогда случайная выборка производится отдельно из каждой группы (страты) с учетом ее относительной численности, а полученная в итоге выборка называется стратифицированной случайной выборкой.