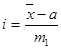Свойства дисперсии. 1. Если из всех значений вариант вычесть какое-то постоянное число, то средний квадрат отклонений не изменится:

1. Если из всех значений вариант вычесть какое-то постоянное число, то средний квадрат отклонений не изменится:

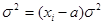
2. Если все значения вариант разделить на какое-то постоянное число, то средний квадрат отклонений уменьшиться в а раз:

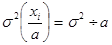
3. Если средний квадрат отклонений от любой величины а – которая отличается от средней арифметической х, то он будет всегда больше среднего квадрата отклонений от средней арифметической: 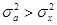, но больше на определенную величину, а эта величина определена, как квадрат разности между средней и этой, условно взятой величиной:

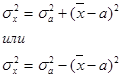
используя 2-ое свойство дисперсии в математической статистике можно рассчитать дисперсию способом моментов. Средний квадрат отклонений от средней величины имеет свойства min, т.е. дисперсия от средней всегда меньше дисперсий исчисляемых от других величин. В этом случае, если а – постоянное число = 0, то, следовательно, средний квадрат отклонений будет определяться по формуле:

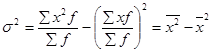
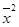- ср. квадрат значений признака;

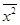- квадрат среднего значения признака.

Значит, средний квадрат отклонений 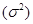равен разности между средним квадратом значения признака и квадратом ср. значения признака.

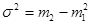
Также способ моментов называется способом отсчета от условного нуля. Данный способ можно применять только в тех случаях, если в вариационных интервальных рядах интервалы одинаковы.

Используя 2-ое свойство дисперсии, разделив все варианты на величину интервала, получим формулу дисперсии:

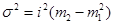
где i – величина интервала для данной совокупности 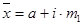;