
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 1. Определить, являются ли следующие предложения высказываниями и найти их истинностные значения.
|
|
1. Определить, являются ли следующие предложения высказываниями и найти их истинностные значения.
а) Функция у = x3 монотонно возрастает на множестве R действительных чисел;
б) Функция у = х2 ― нечетная функция;
в) х2 + у2> 0 для любого х;
г) существует такое действительное число, что 2х + 5=19;
д) любые три отрезка могут быть сторонами треугольника;
ж) х + у = у + х.
2. Выделить структуру следующих высказываний и определить их истинностные значения:
а) диагонали ромба взаимно перпендикулярны и делят углы пополам;
б) если сумма цифр числа делится на 3, то и само число делится на 3;
в) натуральное число не может быть одновременно простым и составным;
г) касательная, проведенная к окружности, перпендикулярна к радиусу, проведенному в точку касания.
3. Построить таблицы истинности для следующих формул исчисления высказываний:
а)  ; б)
; б) 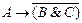 ;
;
в) 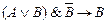 ; г)
; г) 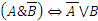 ;
;
д) 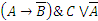 ; е)
; е) 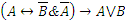 .
.
Равносильность формул. Виды формул
Среди формул логики высказываний есть такие, которые при всех наборах высказывательных переменных принимают значение 1 (истина). Такие формулы называются тавтологиями или логическими законами. Это, например, формулы A∨ 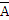 ,
,
А& (А→ В)→ В, (А→ В)↔ (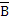 →
→ 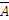 ) и т.д. Они играют особую роль, ибо выражают логическую структуру таких высказываний, которые истинны в силу только этой своей структуры.
) и т.д. Они играют особую роль, ибо выражают логическую структуру таких высказываний, которые истинны в силу только этой своей структуры.
Построив таблицу истинности любой формулы, всегда можно выяснить, является ли она тавтологией или нет, причем, очевидно, достаточно найти хотя бы один набор, при котором формула будет ложной, чтобы сделать вывод о том, что эта формула не тавтология.
Помимо понятия сложного высказывания и связанного с ним понятия формулы, важное значение в логике высказываний имеет отношение равносильности (по-другому ― эквивалентности) формул.
О п р е д е л е н и е: Две формулы от одних и тех же высказывательных переменных называются равносильными, если они принимают одинаковые значения истинности при всех возможных наборах значений истинности входящих в них высказывательных переменных.
Отношение равносильности обозначается знаком ⇔. Из определения следует, что равносильные формулы имеют одинаковые таблицы истинности, поэтому проверка равносильности двух формул сводится к составлению их таблиц истинности и анализа этих таблиц.
Выясним для примера, будут ли равносильными следующие формулы:
1) A& (B∨ C) и (A& B)∨ (A& C)
2)(А→ В)& С и А→ (В& С)?
Для этого составим таблицы истинности этих формул и сравним их:
| [A] | [B] | [С] | [A& (B∨ C)] | [(А& В)∨ (A& C)] | [(A→ B)& C] | [А→ (В& C)] |
Первая пара формул оказалась равносильной, а вторая нет (см. 8 строку таблицы). Последний пример показывает важность скобок: различная последовательность выполнения логических операций может приводить к неравносильным формулам. Поэтому логические операции принято выполнять в следующей последовательности:  , &, ∨, →, ↔, если скобки в данной формуле не расставлены.
, &, ∨, →, ↔, если скобки в данной формуле не расставлены.