
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения.
|
|
1. Доказать:
а) А \ (В 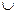 С) = (А \ В) \ С;
С) = (А \ В) \ С;
б) А \ (В \ С) = (А \ В) 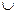 (А
(А 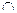 С);
С);
в) (А 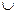 В) \ С = (А \ С)
В) \ С = (А \ С) 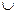 (В \ С);
(В \ С);
г) (А 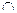 В)
В) 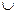 (А \В) = А;
(А \В) = А;
е) А\B=А\(В 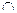 А);
А);
ж) А 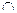 (В \ С) = (А
(В \ С) = (А 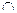 В) \ С;
В) \ С;
и) (А \ В) \ С = (А \ С) \ (В \С);
к) (А\В) = А 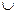 (В
(В 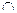 А);
А);
л) (А 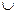 В
В 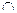 С)=А
С)=А 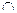 (В
(В 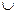 С).
С).
2. Решить систему:
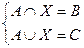 ,
, 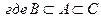
Элементы комбинаторики.
Перестановки, размещения, сочетания
Пусть даны два произвольных множества A и B.
О п р е д е л е н и е 1. Декартовым (прямым) произведением множеств А и В называют множество, состоящее из всех упорядоченных пар вида 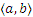 , где
, где  и
и 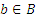 .
.
Символически это множество записывают так:
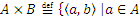 ,
, 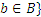
П р и м е р 1: Если А={1, 2, 3}, а В={0, 4}, то
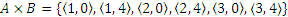 ;
;
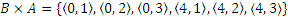 .
.
Видим, что в общем случае 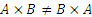 .
.
П р и м е р 2: 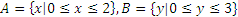 .
.
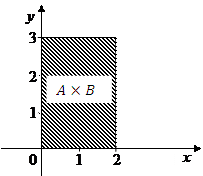 |
П р и м е р 3: R 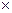 R = R2 ― плоскость (двумерное пространство); R
R = R2 ― плоскость (двумерное пространство); R 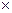 R
R 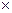 R = R3 ― трехмерное пространство.
R = R3 ― трехмерное пространство.
З а м е ч а н и е: Если 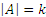 , а
, а 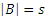 , то
, то 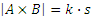 .
.
Прямое произведение можно определить и для нескольких множеств 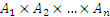 :
:
О п р е д е л е н и е 2.
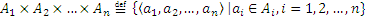 .
.
Аналогичным образом можно ввести понятие декартовой степени множества А:
О п р е д е л е н и е 3.
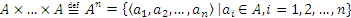 .
.