
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Треугольник Паскаля
|
|
Существует эффективный способ вычисления значений 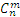 при различных конкретных значениях n и m.
при различных конкретных значениях n и m.
Выпишем в первой строке значение  . Во второй строке выпишем значения
. Во второй строке выпишем значения 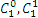 то есть числа 1, 1. В третьей строке выпишем значения
то есть числа 1, 1. В третьей строке выпишем значения 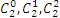 , то есть, соответственно, числа 1, 2, 1. В следующей строке будут значения
, то есть, соответственно, числа 1, 2, 1. В следующей строке будут значения 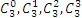 , ― соответственно, числа 1, 3, 3, 1. Каждая последующая строка будет содержать все значения
, ― соответственно, числа 1, 3, 3, 1. Каждая последующая строка будет содержать все значения 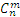 при значениях m = 0, 1, …, n для n = 4, 5,...
при значениях m = 0, 1, …, n для n = 4, 5,...
Заполнение каждой строки, начиная с третьей, происходит следующим образом, в соответствии со свойствами сочетания:
1. Крайние слева и справа элементы любой строки равны 1 (свойство 1).
2. Каждый внутренний элемент строки равен сумме соседних с ним слева и справа элементов предыдущей строки (свойство 4).
Получаем следующую фигуру (при n = 0, 1, 2, З, 4, 5):
n = 0 1
n = 1 1 1
n = 2 1 2 1
n = 3 1 3 3 1
n = 4 1 4 6 4 1
n = 5 1 5 10 10 5 1
Построен так называемый треугольник Паскаля для n от 0 до 5. Его построение по описанному принципу может быть продолжено как угодно далеко. В любой строке треугольника равны любые два числа, равноотстоящие от концов (по свойству 3).
Заметим, что самая верхняя строка имеет номер 0; следующая ― номер 1 и т. д.; номер любой строки, начиная со второй, совпадает с числом, следующим за левой единицей. Кроме того, в любой строке с номером n сумма всех ее членов равна 2n, Это следует из свойства 2.
Треугольник Паскаля позволяет находить без вычислений по формуле любое значение 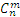 . Например, найдем
. Например, найдем 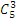 . Для этого ищем строку, в которой после левой единицы находится число 5, затем, начиная от этого числа, отсчитываем третье; это и будет искомое значение. Таким образом,
. Для этого ищем строку, в которой после левой единицы находится число 5, затем, начиная от этого числа, отсчитываем третье; это и будет искомое значение. Таким образом, 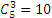 .
.