Необходимые и достаточные условия

Теорема ― высказывание, истинность которого устанавливается при помощи рассуждения (доказательства), проводимого на основе законов логики.

Математические теоремы чаще всего носят общий характер, то есть доказывается, что все элементы некоторого множества обладают общим свойством или свойствами. Например. «Во всяком параллелограмме диагонали в точке пересечения делятся пополам». Логическая структура этой теоремы имеет вид: 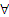x ∈ M P(x).

Это наиболее общая форма записи теорем. Однако часто предикат Р(х) имеет вид импликации А(х) → В(х), поэтому обычно теорема записы­вается в виде: (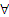 x ∈ M)(A (x) → B (x)), который называют стандартным видом.

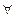( x ∈ M) называют разъяснительной частью этой теоремы,
А(х) ― условием теоремы, В(х) ― заключением теоремы.

Разъяснительная часть теоремы обычно начинается со слова «пусть», после чего разъясняется, об элементах какого множества пойдет речь, что означает каждый введенный символ. Переход от разъяснительной части теоремы к условию отличается словосочетанием «тогда, если», после чего указывается, что представляет из себя высказывательная форма А(х).

Формулировка заключения теоремы начинается после частицы «то».

Например, «Пусть ABCD ― произвольный четырехугольник. Тогда, если ABCD ― ромб, то диагонали ABCD ― перпендикулярны».

Следует заметить, что разъяснительная часть теоремы часто отсутствует, когда понятно, элементы какого множества рассматриваются в теореме.

С любой данной теоремой стандартного вида можно соотнести еще четыре утверждения:

1. ( 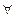x) (А(х) → В(х)) ― прямая теорема;

2. ( 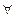x) (В(х) → А(х)) ― обратная теорема;

3. ( 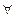x) ( 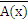→ 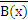) ― противоположная теорема;

4. ( 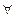x) ( 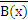→ 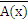) ― обратная к противоположной теорема.

Заметим, что 1 и 4, 2 и 3 теоремы образуют в паре закон контрапозиции, поэтому логически эквивалентны. На практике, как правило, обычно доказывают прямую и (или) обратную теорему.

Если истинна теорема (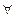 x) (А(х) → В(х)), то В(х) является логическим следствием посылки А(х). В этом случае говорят, что В(х) следует из А(х) и понимают это так, что всегда, когда истинно А(х) будет истинным и В(х) (множество истинности предиката А(х) содержится во множестве истинности предиката В(х) и записывается так: А(х) ⇒ В(х).

Таким образом, доказать теорему стандартного вида ― это означает установить отношение следования между условием и заключением. Если верна теорема (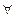 x) (А(х) → В(х)), то А(х) называют достаточным условием для В(х), а В(х) ― необходимым условием для А(х).

Если наряду с прямой теоремой будет верна и обратная теорема (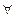 x) (В(х) → А(х)), то В(х) становится необходимым и достаточным условием для А(х). Если в формулировке теоремы есть словосочетание «тогда и только тогда», «необходимо и достаточно», то это «сигнал» того, что придется доказывать прямую и обратную теорему.

Например, теорема: «Параллелограмм является ромбом тогда и только тогда, когда его диагонали перпендикулярны» имеет структуру (А(х) ↔ В(х)).

1. Необходимость В(х) (доказательство прямой теоремы): «Если параллелограмм ― ромб, то его диагонали перпендикулярны».

2. Достаточность В(х) (доказательство обратной теоремы): «Если диагонали параллелограмма перпендикулярны, то он является ромбом».

Так как обе эти теоремы верны, то перпендикулярность диагоналей параллелограмма является необходимым и достаточным условием того, чтобы он был ромбом.

Вопросы для самоконтроля

1. В чем суть метода доказательства от противного?

2. Что называют необходимым условием, достаточным, необходимым и достаточным?