Правило произведения

В математике важную роль играют комбинаторные задачи, связанные с подсчетом числа элементов различных конечных множеств, перебором конечного числа вариантов и т.п.

Одним из основных правил, которые применяются при решении таких задач, является правило произведения.

Пусть элемент 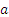можно выбрать 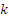способами, а элемент 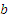― 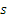способами, тогда пару элементов 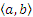можно выбрать 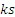способами. Это правило следует из определения декартова произведения двух множеств.

З а м е ч а н и е: Это правило распространяется и на 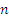множеств.

Приведем примеры решения комбинаторных задач с помощью правила произведения.

З а д а ч а 1. Пусть дан упорядоченный набор длины 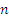, т.е. 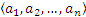, каждый элемент которого может принимать одно из двух значений (например, 0 или 1). Требуется узнать, сколько будет таких наборов (их называют двоичными). Для решения построим клетку с 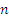ячейками, каждую из которых можно заполнить двумя способами (например, 0 или 1; или «и» и «л» и т.п.):

Следовательно, число двоичных наборов длины n равно 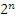. В частности, таблица истинности для логической формулы с n высказывательными переменными имеет 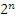строк, так как каждая строка таблицы представляет собой двоичный набор длины n.

З а д а ч а 2. Пусть дано множество 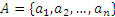. Нужно определить число всех его подмножеств 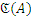. Пусть 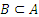. Тогда этому подмножеству можно поставить в соответствие двоичный набор длины n, в котором на i -ом месте стоит 1, если 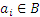, либо 0, если 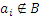. Тогда .

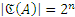Перестановки, размещения и сочетания

Перестановки. Одна из наиболее распространенных комбинатор­ных задач такова: сколькими способами можно переставить элементы некоторого конечного множества? Например: сколько 9-значных чисел с различными цифрами можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9?

При каждой перестановке n- элементного множества образуется упорядоченный набор длины n, все элементы которого различны. Число всех возможных перестановок в данном множестве совпадает с числом всех таких наборов.

О п р е д е л е н и е 4: Перестановкой из n элементов называется упоря­доченный набор длины n с различными элементами, взятыми из неко­торого n- элементного множества.

Число перестановок из n элементов обозначают Р_n. Выведем фор­мулу для вычисления Р_n.

Пусть некоторое множество М состоит из n элементов. Рассмотрим произвольную перестановку элементов этого множества, то есть упорядоченный набор (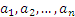), где а_i ∈ М. Элемент а₁ в этом наборе можно выбрать n различными способами (взять любой элемент из множества M); элемент а₂ выбирается n-1 способами (так как один элемент уже использован для а₁, а элементы в перестановке не повторя­ются); а₃ выбирается n-2 способами («заняты» два элемента) и т.д. По­следний элемент а_n можно выбрать только одним способом. По прави­лу произведения, будет всего 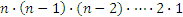указанных набо­ров.

Произведение 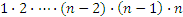, где n ― натуральное число, большее 1, называется n-факториалом и обозначается n! Дополнитель­но полагают: 1! =0! =1. Таким образом, .

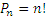Получена формула числа перестановок из n элементов. Применяя эту формулу, можно, в частности, получить, что из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 можно составить 9!, то есть 362880 9-значных чисел с различными цифрами.

Размещения. Другой важный тип комбинаторной задачи можно продемонстрировать на следующем примере: сколькими способами из 10 учебных предметов можно составить расписание занятий на один день, включив в него 4 различных предмета? Очевидно, что один вари­ант расписания может отличаться от другого как предметами, так и по­рядком их следования. Поэтому данную задачу можно сформулировать так: сколько существует упорядоченных наборов длины 4 с различными элементами, взятыми из 10-элементного множества? Число всех таких наборов называется числом размещений из 10 элементов по 4.

О п р е д е л е н и е 5: Размещением из n элементов по m (m≤ n) называет­ся упорядоченный набор длины m различными элементами, взятыми из некоторого n -элементного множества.

Еще раз напомним, что упорядоченные наборы с одними и теми же элементами, но разным порядком их следования считаются различными.

Обозначим число размещений из n элементов по n через 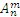и вы­ведем формулу для вычисления .

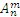Рассмотрим n -элементное множество M и произвольный упорядо­ченный набор (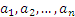), где a_i ∈ M для всех i, i = =1, 2,..., m. Элемент а₁ выбирается n различными способами; a₂ выбирается n-1 способами и т.д. Последний элемент а_m можно выбрать
(n - (m - 1)), то есть (n - m + 1) способами. По правилу произведения, имеется всего 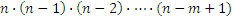указанных наборов.

Искомая формула имеет вид:

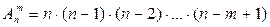(1)

Заметим, что произведение в правой части состоит в точности из m множителей. Это облегчает применение формулы.

Вернемся к задаче о расписании. Число всех вариантов расписания можно посчитать по формуле (1): .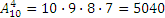

Имеет место другая формула для :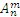

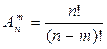
Для ее вывода достаточно преобразовать правую часть формулы (1).

Сочетания. Рассмотрим теперь такую задачу: сколькими спосо­бами можно из 10 учебных предметов выбрать 4 для составления распи­сания на день? Заметим, что в этой задаче, в отличие от задачи преды­дущего пункта, не требуется составлять расписание, то есть упорядочи­вать предметы. Нужно узнать, сколькими способами из множества, со­стоящего из 10 элементов, можно выбрать 4-элементное подмножество (а не упорядоченный набор). Число таких подмножеств называют чис­лом сочетаний из 10 элементов по 4.

О п р е д е л е н и е 6: Сочетанием из n элементов по m
(m≤ n) называет­ся m -элементное подмножество n -элементного множества.

Подчеркнем, что в данном случае не различаются подмножества, со­стоящие из одних и тех же элементов, в каком бы порядке эти элементы не перечислялись.

Число сочетаний из n элементов по m обозначают 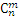. Выведем формулу для нахождения этого числа.

Пусть дано множество из n элементов. Возьмем произвольное m -элементное подмножество этого множества и составим из него все воз­можные упорядоченные наборы. Их будет m! Проделав такое действие с каждым подмножеством, получим множество всех упорядоченных на­боров длины m, то есть всех размещений из n элементов по m. Их число .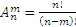

Таким образом, 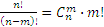. Отсюда: .

Иногда последнюю формулу записывают по-другому:

.

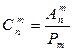Применив полученную формулу, найдем :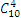

.

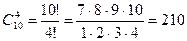Число 210 дает ответ задачи, поставленной в начале этого пункта.