Соответствия и отношения

Основные знания, умения и навыки, которыми должны овладеть студенты в процессе изучения этой темы:

· понимать смысл неопределяемых понятий «соответствие», «отношение»;

· знать свойства соответствий и отношений, уметь их определять и приводить конкретные примеры;

· знать основные типы соответствий и отношений.

Основные понятия темы: соответствие, отношение.

Пусть даны два произвольных множества A и B.

О п р е д е л е н и е 1. Декартовым (прямым) произведением множеств А и В называют множество, состоящее из всех упорядоченных пар вида 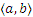, где и .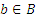

Символически это множество записывают так:

,

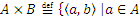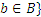
П р и м е р 1: Если А={1, 2, 3}, а В={0, 4}, то

;

.

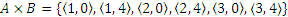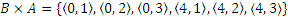Видим, что в общем случае .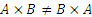

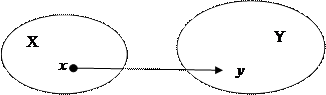
Пусть даны два произвольных множества X, Y.

Тройка множеств 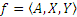, где 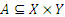, будем называть бинарным соответствием между множеством X и Y, множество A ― его графиком, множество X ― областью отправления, Y ― областью прибытия.

Если 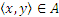, то говорят, что элемент x находится с элементом y в соответствии f и пишут x f y, то есть .

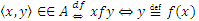З а м е ч а н и е: Часто понятие бинарного соответствия определяют как любое подмножество А множества 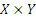, то есть отождествляют его с графиком соответствия.

Множество 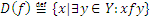называют областью определения соответствия f.

Множество 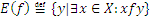называют областью значения соответствия f.

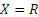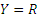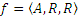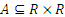П р и м е р 1. Пусть , . Тогда тройка множеств , где и 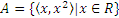будет задавать соответствие между множествами R и R, графиком которого будет парабола. D(f)=R, E(f)=R⁺. .

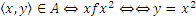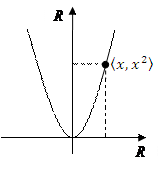
П р и м е р 2: Пусть 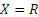, 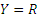. . 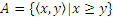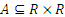, 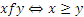. График этого соответствия пред­ставляет собой полуплоскость.

Множество 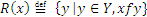называют полным образом элемента x при соответствии f.

Множество называют полным прообразом элемента у при соответствии f.

Из определения 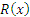и 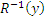следует, что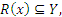
.

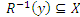П р и м е р 3: Пусть X ― множество студентов в аудитории, У ― множе­ство столов, за которым они сидят. Зададим соответствие х f у «студент x сидит за столом y». Тогда:

1. Областью отправления этого соответствия будет множество всех студентов в аудитории;

2. Областью определения ― множество студентов, которые сидят за столами;

3. Областью прибытия ― множество столов в аудитории.

4. Областью значений ― множество столов, за которыми сидит хотя бы один студент;

5. Графиком соответствия будет множество пар «студент- стол»

6. Полным прообразом студента х будет стол, за которым он сидит;

7. Полным прообразом стола у будут все студенты, которые за ним сидят.

П р и м е р 4:

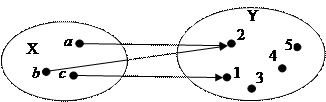Этот рисунок задает соответствие между множествам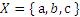и:

и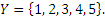

График этого соответствия . , , , , , , , .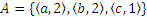

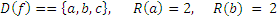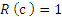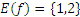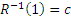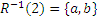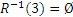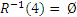Из рассмотренных выше примеров видно, что соответствие может быть задано:

а) путем указания подмножества 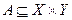(графически);

б) аналитически; х f у 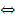у = f (х);

в) с помощью графов или таблиц.

Графом называют множество точек, некоторые пары из которых соединены линиями с направлениями (см. пример 4).

Операции над соответствиями

Понятие бинарного соответствия тесно связано с понятием двухме­стного предиката. Если Р(х, у) ― двухместный предикат, в котором перемен­ная х пробегает множество X, переменная у ― множество У, а Т ― множество истинности этого предиката, то тройка множеств 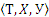будет задавать соответствие между X и У.

Связь между понятиями двухместного предиката и бинарного соот­ветствия та же, что и между характеристическим свойством (одноместным предикатом) и множеством. Эта связь позволяет перенести на соответствия все понятия, рассмотренные в предыдущем параграфе для предикатов.

Пусть даны два соответствия: 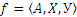, 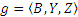. Эти соответствия называются противоположными, если их графики взаимно дополняют друг друга в множестве Х У, или на «языке» предика­тов ― соответствующие им предикаты Р(х, у) и Q (х, у), взаимно отрицают друг друга.

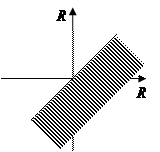
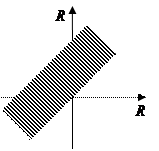
Например, для соответствия «х f у ⇔ х < у» противоположным бу­дет соответствие «х f у ⇔ х ≥ у».

Действительно, графики этих соответствий ― взаимно дополняющие множества 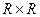― и отрицание предиката «x< y» есть предикат «x≥ y».

Объединением соответствий f и g называют соответствие, графиком которого является объединение графиков А и В 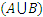и которому соответствует дизъюнкция предикатов Р(х, у) и Q(x, y): (Р(х, у) 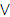Q(x, у)).

Аналогично определяется пересечение соответствий.

Например, для соответствий «хfу 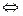х 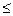у» и «хfу⇔ ⇔ х≥ у» их объединением будет соответствие «хhу⇔ ⇔ ((х у) ⋁ (x 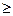у)) с графиком R 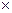R, а пересечением ―
«х S у ⇔ (х 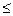у) & (х 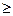у)» с графиком А ={{х, х} / х R}.

Для каждого соответствия 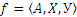можно определить обратное соответствие f 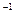между У и X следующим образом: у f ^-1 x 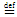x f у, иначе ― пара 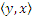принадлежит графику соответствия f ^-1 тогда и толь­ко тогда, когда пара .

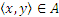Можно сказать, что граф соответствия f ^-1 получается из графа соответствия f изменением направления всех стрелок.

Например, если х f у ⇔ «прямая х касается окружности у», то у f ^-1 x ⇔ «окружность у касается прямой х».

Определим операцию композиции двух соответствий , :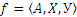

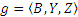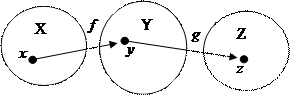
Обозначим через С график композиции соответствий f и g.

Тогда

.

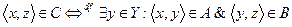На «языке» графов это означает, что точки (х) и (z) соединяются стрелками в том случае, если соединены стрелками точки (х) и (у), (у) и (z).

Короче ― .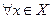

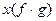
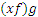П р и м е р: Пусть хfу ⇔ «у=х²», ygz ⇔ «z=y+2».

Тогда х(fg)z ⇔ «z = х² + 2».