
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Операции на множествах и их свойства
|
|
Основные знания, умения, и навыки, которыми должны овладеть студенты в процессе изучения данной темы:
· знать основные операции на множествах;
· знать определение бинарной операции на множестве;
· знать и понимать свойства бинарных операций.
Основные понятия темы: n- арная операция, бинарная операция.
О п р е д е л е н и е 1: Отображение 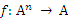 множества Аn в множество А называется n-арной (n-местной) операцией f, заданной на множестве А. Число n называется рангом операции.
множества Аn в множество А называется n-арной (n-местной) операцией f, заданной на множестве А. Число n называется рангом операции.
Из этого определения следует, что n- арная операция является всюду определенным, функциональным соответствием, т.е. всюду определенной функцией n переменных со значением из множества А.
Действие этой функции на элементы множества А обозначают так:
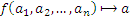
Элементы 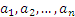 называют операндами, а значение функции
называют операндами, а значение функции 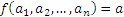 ― результатом операции f.
― результатом операции f.
В частности, при n = 0 операцию f называют нуль-арной, ее смысл состоит в том, что на множестве А выделяется (фиксируется) некоторый элемент. При n = 1 операцию f называют унарной, она является отображением f: А  А. При n = 2 ― бинарной, она является отображением f: А2
А. При n = 2 ― бинарной, она является отображением f: А2  А. При n = 3 ― тернарной, она представляет собой отображение f: А3
А. При n = 3 ― тернарной, она представляет собой отображение f: А3  А.
А.
Например, нуль-арными операциями будут: операция фиксации 1 на множестве N натуральных чисел, или операция фиксации 0 на множестве Z целых чисел; унарными операциями являются операция возведения в целую степень, а⟼ аn на множестве Q рациональных чисел, или операция взятия противоположного элемента а ⟼ (-а) на множестве Z целых чисел.
В математике чаще всего рассматриваются бинарные операции. Результат бинарной операции f(a, b) обычно записывают в виде a f b. Вместо буквы f в конкретных случаях используют специальные знаки и символы:
+, –, ∙,: ― для операций над числами;
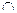 ,
, 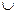 , \ ― для операций над множествами;
, \ ― для операций над множествами;
&, ∨,  ,
,  ― для операций над высказываниями;
― для операций над высказываниями;
∘ ― для композиции отображений.
Из определения n- арной операции следует, что соответствие
f: А2  А является бинарной операцией тогда и только тогда, когда истинны следующие условия:
А является бинарной операцией тогда и только тогда, когда истинны следующие условия:
1. 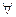 (а, b)
(а, b)  А2
А2 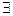 с
с  А | a f b = с ― условие выполнимости операции на множестве (всюду определенности).
А | a f b = с ― условие выполнимости операции на множестве (всюду определенности).
2. 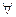 (а, b)
(а, b)  А2
А2 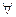 с, d
с, d  A | (a f b = с) & (a f b = d)
A | (a f b = с) & (a f b = d) 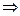 (с = =d) ― условие однозначности операции (функциональности).
(с = =d) ― условие однозначности операции (функциональности).
З а м е ч а н и е. Если условие 2) не соблюдается, т.е.
3. 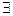 (а, b)
(а, b)  А2
А2 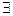 с, d
с, d  A | (a f b = с) & (a f b = d)& (с
A | (a f b = с) & (a f b = d)& (с 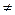 d), то соответствие f не является операцией, более того ― отображением.
d), то соответствие f не является операцией, более того ― отображением.
Если не соблюдается условие 1), соответствие f не является всюду определенным, т.е. 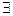 (а, b)
(а, b)  А2 |
А2 | 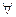 с
с  A, (a f b
A, (a f b 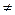 c) или
c) или 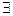 (а, b)
(а, b)  А2 | (a f b = с) & (с
А2 | (a f b = с) & (с 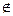 A), то мы приходим к следующему определению:
A), то мы приходим к следующему определению:
О п р е д е л е н и е 2: Функцию f: А2  А называют частичной бинарной операцией на множестве А (частично выполнимой на множестве А операцией), если она не является всюду определенной.
А называют частичной бинарной операцией на множестве А (частично выполнимой на множестве А операцией), если она не является всюду определенной.
П р и м е р 1: Арифметическая операция вычитания целых чисел на множестве натуральных чисел N не всегда выполнима, так как 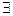 (а, b)
(а, b)  N2 | (a-b)
N2 | (a-b) 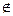 N, то есть эта операция ― частична. В то же время она ― однозначна, так как
N, то есть эта операция ― частична. В то же время она ― однозначна, так как
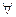 (а, b)
(а, b)  N2
N2 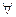 с, d
с, d  N | (a – b = с) & (a – b = d)
N | (a – b = с) & (a – b = d) 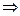 (с = d)
(с = d)
П р и м е р 2: Арифметическая операция деления рациональных чисел на множестве Z целых чисел также частично выполнима. Например, результат деления целых чисел 3 и 5 не является целым числом.
О п р е д е л е н и е 3: Если на множестве А задана бинарная операция * и непустое подмножество В множества А таково, что 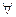 а, b
а, b  В, а * b
В, а * b  В, т.е операция *, заданная на А, выполнима на его подмножестве В, то такое подмножество В называется замкнутым относительно операции *. В этом случае говорят также, что операция * не выводит за пределы множества В.
В, т.е операция *, заданная на А, выполнима на его подмножестве В, то такое подмножество В называется замкнутым относительно операции *. В этом случае говорят также, что операция * не выводит за пределы множества В.
П р и м е р 3. Относительно операции умножения целых чисел множество всех положительных целых чисел замкнуто, а множество всех отрицательных целых чисел незамкнуто.
Иногда свойство замкнутости множества относительно операции считают эквивалентным свойству выполнимости операции на множестве.