
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовых множествах
|
|
Важными свойствами бинарной операции являются свойства ассоциативности, коммутативности, существования нейтрального элемента (левого, правого, двухстороннего), существования обратного элемента (левого, правого, двухстороннего), наличие нулей и идемпотентов. Сформулируем основные свойства бинарных операций в виде условий, называемых также аксиомами:
А1. Аксиома ассоциативности:
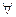 а, b, с
а, b, с  А, (а * b) * с = а * (b * c);
А, (а * b) * с = а * (b * c);
А2. Аксиома коммутативности:
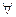 а, b
а, b  А, а * b = b * a;
А, а * b = b * a;
A3. Аксиома существования левого нейтрального элемента:
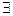 e'
e'  A |
A | 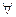 a
a  A, e' * a = a;
A, e' * a = a;
A4. Аксиома существования правого нейтрального элемента:
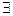 e''
e''  A |
A | 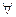 a
a  A, a * e''= a;
A, a * e''= a;
А5. Аксиома существования нейтрального элемента (двухстороннего):
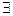 е
е  А |
А | 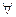 а
а  А, е * а = а * е = а;
А, е * а = а * е = а;
А6. Аксиома левого симметричного элемента:
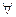 a
a  A
A 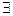 а'
а'  А | а' * а = e;
А | а' * а = e;
А7. Аксиома правого симметричного элемента:
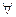 a
a  A
A 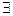 а''
а''  А | а * а'' = e;
А | а * а'' = e;
А8. Аксиома существования симметричного элемента (двухстороннего):
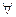 a
a  A
A 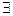
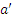
 А |
А | 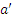 * а = а *
* а = а * 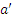 = е.
= е.
О п р е д е л е н и е 4: Говорят, что бинарная операция * на множестве А:
· коммутативна, если выполняется условие А2,
· ассоциативна, если выполняется условие А1`,
· обладает нейтральным элементом (левым, правым), если выполняется А5 (A3, А4),
· обратима (слева, справа), если выполняется А8 (А6, А7).
П р и м е р 4. Исследовать свойства бинарной операции *, заданной на множестве Q по правилу:
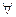 a, b
a, b  Q, а * b = а – ab + 1.
Q, а * b = а – ab + 1.
Р е ш е н и е:
1. Проверка условия выполнимости. Так как сумма, произведение, разность рациональных чисел являются рациональными числами, то результат операции а – ab + 1 есть рациональное число. Операция * выполнима на Q.
2. Проверка условия однозначности. Операции сложения, умножения, вычитания рациональных чисел ― однозначны. Следовательно, и операция *, которая определяется через них, будет однозначной.
3. Проверка аксиомы ассоциативности. Возьмем любую тройку элементов а, b, с из множества Q и проверим выполнимость равенства: (а * b) * с = а * (b * с). Раскрывая левую часть этого равенства, получаем:
(а * b) * с = (а – ab + 1) *c = (a – ab +1) – (a – ab + 1)с+1 =
= a – аb – aс + abc – c + 2.
Раскрывая правую часть рассматриваемого равенства, получаем:
а * (b * с) = а * (b ― bc + 1) = а ― а(b ― bc + 1) + 1 =
=1– ab+ abc.
Результаты различны, поэтому операция * неассоциативна.
4. Проверка аксиомы коммутативности:
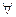 а, b
а, b  Q, а * b = b * a.
Q, а * b = b * a.
Так как a*b = a–ab+1, b*a= b – ba + 1, то при а 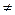 b результаты различны. Итак, операция * некоммутативна.
b результаты различны. Итак, операция * некоммутативна.
5. Проверка наличия нейтральных элементов:
а) Из аксиомы A3 имеем: х * а = а или х – ха + 1 = а, откуда х = –1. Следовательно, существует левый нейтральный элемент е' =1.
б) Из аксиомы А4 имеем: а * х = а или а – ах + 1 = а, откуда 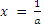 . Здесь х зависит от а. Следовательно, правого нейтрального элемента нет.
. Здесь х зависит от а. Следовательно, правого нейтрального элемента нет.
в) Из пунктов а) и б) следует, что нейтрального (двухстороннего) элемента нет.
6. Проверка наличия симметричных элементов.
Для выполнения аксиом А6 и А7 необходимо наличие двухстороннего нейтрального элемента e относительно заданной операции. Так как такой элемент отсутствует, то операция * не обладает симметричными элементами.
Упражнения
1. Является ли операцией и какого ранга вычитание на множестве R? В случае положительного ответа перечислить основные свойства операции.
2. Исследовать свойства операции *, заданной на множестве R формулами:
а) а * b = (а + b)2; б) а * b = а2 +1;
в) а * b = 2а + b –1; г) а * b = ab–a+b;
д) а * b = ab; е) а * b = a2b–ab2.
Зачетная контрольная работа
1. Доказать:
1) 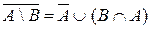 ;
;
2) А \ (В 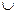 С) = ((А \ В) \ С);
С) = ((А \ В) \ С);
3) A \ (B \ C) = (A \ B) 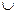 (A
(A 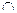 C);
C);
4) А \ В = А \ (В 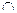 А);
А);
5) А \ (А \ В) = А 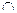 В;
В;
6) А 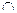 (В \ С) = (А
(В \ С) = (А 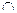 В) \ (А
В) \ (А 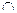 С);
С);
7) А 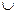 В = А
В = А 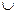 (В \ А);
(В \ А);
8) (А 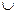 В) \ С = (А \ С)
В) \ С = (А \ С) 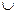 (В \ С);
(В \ С);
9) (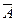
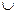 В)
В) 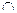 А=A
А=A 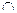 B;
B;
10) (А \ В)\С = (А\С)\ (В\С).
2. Построить таблицу истинностных значений данных формул исчисления высказываний:
1) А & 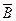 ∨
∨ 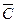 ; 6) A∨
; 6) A∨ 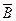
 C;
C;
2) A ∨ (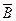

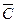 ); 7)
); 7) 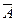 &
& 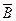
 C;
C;
3) (А  В) ∨
В) ∨ 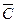
 A; 8) A
A; 8) A 
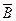 ∨
∨ 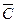 ;
;
4) А & 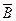

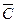 ; 9) A& (B
; 9) A& (B  C);
C);
5) (A  B)& (A∨ C); 10) A
B)& (A∨ C); 10) A  B
B 
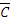 .
.
3. Построить отрицание следующих формул:
1)  ;
;
2) 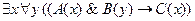 ;
;
3) 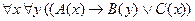 ;
;
4) 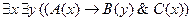 ;
;
5) 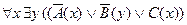 ;
;
6) 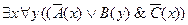 ;
;
7) 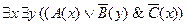 ;
;
8) 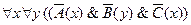 ;
;
9) 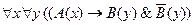 ;
;
10) 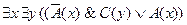 .
.
4. Какими свойствами обладает данное соответствие на множестве R?
1) f: R  R, f: x
R, f: x 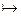 kx + b;
kx + b;
2) f: R  R, f: x
R, f: x 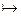 x3;
x3;
3) f: R  R, f: x
R, f: x 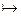
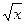 ;
;
4) f: R  R, f: x
R, f: x 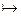 |x|;
|x|;
5) f: R  R, f: x
R, f: x 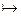 sin x;
sin x;
6) f: R  R, f: x
R, f: x 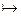 cos x;
cos x;
7) f: R  R, f: x
R, f: x 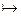 tg x;
tg x;
8) f: R  R, f: x
R, f: x 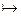 ctg x;
ctg x;
9) f: R  R, f: x
R, f: x 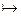 lg x;
lg x;
10) f: R  R, f: x
R, f: x 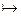 ax, a
ax, a  R.
R.
5. Какими свойствами обладает данное отношение на множестве R?
1) 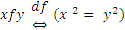 ;
;
2) 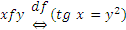 ;
;
3) 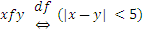 ;
;
4) 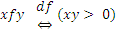 ;
;
5) 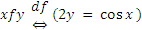 ;
;
6) 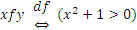 ;
;
7) 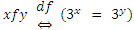 ;
;
8) 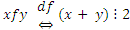 ;
;
9) 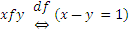 ;
;
10)  .
.
6. Доказать методом математической индукции:
1) 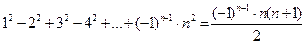 ;
;
2) 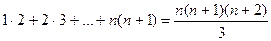 ;
;
3) 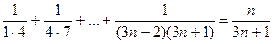 ;
;
4) 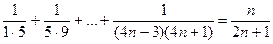 ;
;
5) 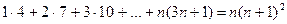 ;
;
6) 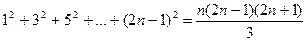 ;
;
7) 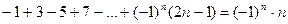 ;
;
8) 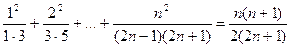 ;
;
9) 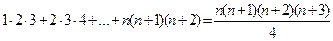 ;
;
10) 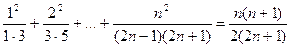 .
.