
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Фактор-множество
|
|
Приведем таблицу классификации отношений по их свойствам:
| Реф-ть | Сим-ть | Антисим-ть | Асим- ть | Транз-ть | Связ- ть | Название |
| + | + | + | Отношение эквивалентности | |||
| + | + | Отношение строгого порядка | ||||
| + | + | + | Отношение нестрогого порядка | |||
| + | + | + | Отношение линейного порядка |
П р и м е р ы: Отношение 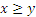 на множестве R ― нестрогого порядка,
на множестве R ― нестрогого порядка, 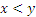 ― строгого порядка, х = у ― отношение эквивалентности.
― строгого порядка, х = у ― отношение эквивалентности.
Систему S непустых подмножеств заданного множества A будем называть разбиением множества А, если каждый элемент множества А принадлежит одному и только одному подмножеству из системы S. Подмножество из S называются смежными классами разбиения S.
С каждым разбиением S мы свяжем бинарное отношение φ на множестве А, полагая, по определению, 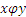 тогда и только тогда, когда x и y принадлежат одному и тому же смежному классу множества А.
тогда и только тогда, когда x и y принадлежат одному и тому же смежному классу множества А.
 Изобразим множество А в виде квадрата, а смежные классы ― в виде прямоугольников, на которые разбивается квадрат. Имеем, что
Изобразим множество А в виде квадрата, а смежные классы ― в виде прямоугольников, на которые разбивается квадрат. Имеем, что 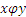 тогда и только тогда, когда x и y принадлежат одному и тому же прямоугольнику. Ясно, что отношение
тогда и только тогда, когда x и y принадлежат одному и тому же прямоугольнику. Ясно, что отношение 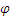 является отношением эквивалентности. Оно называется отношением эквивалентности, отвечающим разбиению S.
является отношением эквивалентности. Оно называется отношением эквивалентности, отвечающим разбиению S.
Совокупность всех смежных классов множества А по отношению эквивалентности 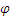 обозначается через
обозначается через 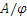 и называется фактор-множеством от А по
и называется фактор-множеством от А по 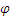 .
.
Однозначное отображение 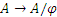 , при котором каждый элемент
, при котором каждый элемент  переходит в содержащий его смежный класс
переходит в содержащий его смежный класс 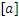 , называется каноническим отображением А на
, называется каноническим отображением А на 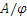 .
.
Упражнения
1. Доказать, что всякое симметричное, транзитивное, всюду определенное отношение является отношением эквивалентности.
2. Построить отношение эквивалентности на множестве Z.
3. Доказать, что отношение 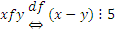 на множестве Z есть отношение эквивалентности. Построить фактор-множество по этому отношению.
на множестве Z есть отношение эквивалентности. Построить фактор-множество по этому отношению.
4. Найти фактор-множество 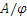 , если:
, если:
а) 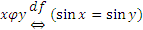 ,
, 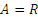 ;
;
б) 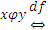 «x и y имеют одинаковые остатки при делении на 7»,
«x и y имеют одинаковые остатки при делении на 7», 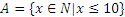 .
.
5. Доказать, что любые два смежных класса из фактор-множества 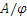 общих элементов не имеют.
общих элементов не имеют.