Отношения

Если дано соответствие 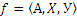и X = Y, то f называют отношением во множестве X. Примерами отношений в R могут служить: 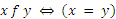; ; 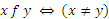; 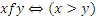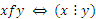и т.п.

Если X = М, где М ― множество прямых, то 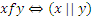; 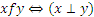и т.д.

Таким образом, отношение есть частный случай соответствия и поэтому все свойства соответствий справедливы и для отношений, однако, для отношений вводятся еще дополнительные свойства такие, как рефлек­сивность, симметричность, транзитивность и т.д.

Отношение f на множестве X называют рефлексивным, если 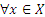, х f x.

П р и м е р 1: Пусть 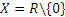, 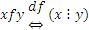. Это отношение рефлексивно, т.к. каждое действительное число, отличное от нуля, делится само на себя, т.е. .

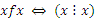Отношение f на множестве X называют антирефлексивным, если 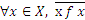, то есть график этого отношения не содержит ни одной пары вида , или ни один элемент не имеет «петли».

П р и м е р 2: Пусть 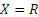, 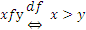. Это отношение антирефлексивно, так как любое действительное число не больше самого себя.

Отношение f на множестве X называют симметричным, если .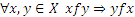

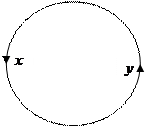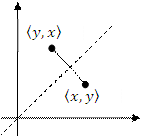
График симметричного отношения вместе с парой 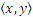содержит и пару 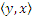, или же: если есть стрелка из х в у, то и есть стрелка и из y в x.

П р и м е р 3: Если X = М, 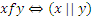, то это отношение будет симметричным, так как если прямая x параллельна прямой y, то и прямая y параллельна прямой x.

Отношение f на множестве X называют асимметричным, если 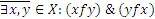одновременно, то есть если график этого отношения содержит пару 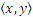, то не содержит пару 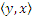или, если из x в y приходит стрелка, то из y в x ее нет.

П р и м е р 4: Пусть 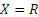, 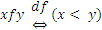. Это отношение асимметрич­но, так как если х < у, то x не может быть больше у.

Отношение f на множестве X называют антисимметричным, если из того, что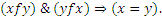

П р и м е р 5: Пусть 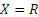, 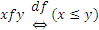. Это отношение антисимметрично.

Ясно, что всякое асимметричное отношение является и антисимметричным, но не наоборот.

Отношение на множестве X называют транзитивным, если 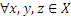из того, что

П р и м е р 6: Отношения х< у, х = у, х > у, х || у — транзитивны.

Отношение f на множестве X называют связным, если

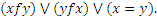
П р и м е р 7: Пусть X = N, 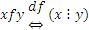. Это отношение рефлексивно, так как 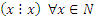, антисимметрично, так как , если 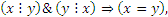транзитивно, так как если 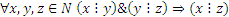, не связно, так как 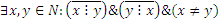, например, :
.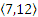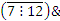
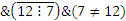