
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Одноканальные СМО с однородным потоком заявок
|
|
Системы и сети массового обслуживания
Одноканальные системы массового обслуживания
ЗАНЯТИЕ 1/1
Принципы работы одноканальных СМО
Одноканальные СМО с однородным потоком заявок
Рассмотрим одноканальную СМО с однородным потоком заявок при следующих предположениях (рис.4.1):
1) СМО содержит один обслуживающий прибор, в котором в каждый момент времени может обслуживаться только одна заявка;
 2) перед прибором имеется накопитель Н неограниченной ёмкости, что означает отсутствие отказов поступающим заявкам при их постановке в очередь О, то есть любая поступающая заявка всегда найдет в накопителе место для ожидания не зависимо от того, сколько заявок уже находится в очереди;
2) перед прибором имеется накопитель Н неограниченной ёмкости, что означает отсутствие отказов поступающим заявкам при их постановке в очередь О, то есть любая поступающая заявка всегда найдет в накопителе место для ожидания не зависимо от того, сколько заявок уже находится в очереди;
3) заявки поступают в СМО с интенсивностью λ;
4) средняя длительность обслуживания одной заявки в приборе равна b, причем длительности обслуживания разных заявок не зависят друг от друга;
5) обслуживающий прибор не простаивает, если в системе (накопителе) имеется хотя бы одна заявка, причем после завершения обслуживания очередной заявки мгновенно из накопителя выбирается следующая заявка;
6) заявки из накопителя выбираются в соответствии с бесприоритетной дисциплиной обслуживания в порядке поступления (ОПП) по правилу «первым пришел – первым обслужен» (FIFO – First In First Out).
7) в системе существует стационарный режим, предполагающий отсутствие перегрузок, то есть нагрузка и, следовательно, загрузка системы меньше 1: y = ρ = λ b < 1.
В качестве расчётной характеристики обслуживания заявок в СМО будем использовать среднее время ожидания заявок. Значения остальных характеристик функционирования СМО легко могут быть рассчитаны с использованием приведенных в разделе 3 фундаментальных соотношений (3.13) – (3.15).
Рассмотрим четыре модели СМО с однородным потоком заявок: экспоненциальную СМО М/М/1 и три неэкспоненциальные СМО типа M/G/1, G/M/1, G/G/1.
1. Характеристики экспоненциальной СМО M/M/1
Пусть заявки, поступающие в одноканальную СМО, образуют простейший поток с интенсивностью λ, а длительность τ b обслуживания заявок распределена по экспоненциальному закону со средним значением b, причём ρ = λ b < 1, то есть система работает в установившемся режиме Такая СМО с однородным потоком заявок называется экспоненциальной.
С использованием метода средних значений [2] или марковской модели (см.п.5.4.4) можно получить следующие выражения для расчета средних значений:
• времени ожидания заявок
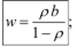 (4.1)
(4.1)
• времени пребывания заявок
 (4.2)
(4.2)
• длины очереди заявок

• числа заявок в системе (в очереди и на обслуживании)

Из последнего выражения вытекает, что среднее число заявок в системе m = l + ρ, где второе слагаемое ρ определяет среднее число заявок, находящихся на обслуживании в приборе. Кроме того, сравнивая выражения (4.1) и (4.2) получим, что u = ρ w.
2. Характеристики неэкспоненциальной СМО M/G/1
Пусть заявки, поступающие в одноканальную СМО, образуют простейший поток с интенсивностью λ, а длительность τ b обслуживания заявок распределена по произвольному закону B(τ) со средним значением b и коэффициентом вариации ν b.
С использованием метода средних значений можно показать, что среднее время ожидания заявок определяется по формуле Поллачека-Хинчина [2]:
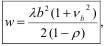 (4.3)
(4.3)
где ρ = λ b < 1 – загрузка системы.
Среднее время пребывания заявок в системе:
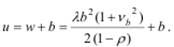
Следует отметить интересную особенность представленных выражений, а именно: средние значения характеристик обслуживания заявок зависят только от двух первых моментов длительности обслуживания заявок и не зависят от моментов более высокого порядка. Другими словами, для того чтобы рассчитать средние характеристики обслуживания, не обязательно знать закон распределения длительности обслуживания заявок – достаточно знать только два первых момента распределения. Можно показать, что для расчета вторых моментов характеристик обслуживания заявок достаточно задать три первых момента длительности обслуживания и т.д. Резюмируя, можно утверждать, что для СМО с простейшим потоком заявок для расчёта первых k моментов характеристик обслуживания необходимо задать (k +1) моментов длительности обслуживания заявок.
3. Характеристики неэкспоненциальной СМО G/M/1
Пусть в одноканальную СМО с интенсивностью λ поступает случайный поток заявок произвольного вида, задаваемый функцией распределения интервалов между заявками A(τ), а длительность τ b обслуживания заявок распределена по экспоненциальному закону B(τ) со средним значением b (интенсивностью µ = 1/b).
СМО G/M/1 является симметричной по отношению к СМО M/G/1, рассмотренной в предыдущем пункте. Однако получение конечного результата в виде аналитического выражения для расчёта среднего времени ожидания, по аналогии с предыдущей моделью, в общем случае, оказывается невозможным. Это обусловлено тем, что среднее время ожидания, впрочем, как и другие числовые моменты, зависит не только от двух первых моментов интервалов между поступающими заявками, но и от моментов более высокого порядка, т.е. от закона распределения интервалов между заявками.
Среднее время ожидания заявок в очереди может быть рассчитано следующим образом [9]:
w=ς b / (1− ς), (4.4)
где ς – единственный в области 0 < ς < 1 корень уравнения
ς =A* (µ − µ ς). (4.5)
Здесь A*(s) – преобразование Лапласа плотности распределения a(τ) интервалов между поступающими в систему заявками:
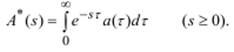
Основная сложность при исследовании СМО G/M/1 заключается в том, что уравнение (4.5) для нахождения ς, в общем случае, является трансцендентным, и невозможно получить выражение для ς в явном виде.
Однако в каждом конкретном случае корень уравнения (4.5) может быть найден с использованием численных методов.
Как сказано выше, средние значения характеристик обслуживания заявок зависят не только от двух первых моментов интервалов между поступающими заявками, но и от моментов более высокого порядка, причем степень влияния соответствующих моментов убывает с увеличением порядка моментов. Другими словами, влияние моментов 4-го порядка менее существенно, чем моментов 3-го порядка и т.д.
Пример 4.1. Проиллюстрируем применение описанного метода расчета к рассмотренной выше СМО M/M/1 с простейшим потоком заявок.
В простейшем потоке интервалы времени между последовательными заявками распределены по экспоненциальному закону, преобразование Лапласа которого имеет вид: 
Тогда уравнение (4.5) примет вид:

После некоторых преобразований получим квадратное уравнение:
µς 2− (λ +µ)ς +λ = 0.
Разделив левую и правую часть этого уравнения на µ, получим:
ς 2− (1+ρ)ς + ρ =0.
Из двух корней ς 1 =1 и ς 2 = ρ последнего уравнения условию 0< ς < 1 удовлетворяет только второй корень. Подставляя его в выражение (4.4) окончательно получим выражение для среднего времени ожидания, совпадающее с известным для СМО M/M/1 выражением (4.1).
ВЫВОД
Средние значения характеристик обслуживания заявок зависят не только от двух первых моментов интервалов между поступающими заявками, но и от моментов более высокого порядка, причем степень влияния соответствующих моментов убывает с увеличением порядка моментов.