
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Анализ свойств одноканальной СМО
|
|
Анализ свойств одноканальной СМО с однородным потоком заявок будем проводить с использованием представленных выше математических моделей в виде формул (4.1 – 4.3), определяющих зависимости характеристик обслуживания заявок от параметров поступления и обслуживания заявок для установившегося (стационарного) режима работы системы.
1. Среднее время ожидания заявок в очереди минимально при постоянной (детерминированной) длительности обслуживания заявок, когда коэффициент вариации длительности обслуживания ν b = 0, и увеличивается с ростом коэффициента вариации (дисперсии) длительности обслуживания. Заметим, что зависимость среднего времени ожидания от коэффициента вариации ν b носит нелинейный характер. Так, например, при экспоненциально распределенной длительности обслуживания, когда ν b =1, среднее время ожидания заявок увеличивается в 2 раза, а при ν b = 2 – в 5 раз, по сравнению с детерминированным обслуживанием.
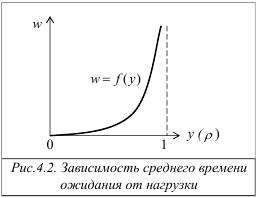 2. Среднее время ожидания заявок существенно зависит от нагрузки y (загрузки ρ) системы (рис.4.2). При y ≥ 1 (ρ → 1) время ожидания заявок возрастает неограниченно: w → ∞, т.е. заявки могут ожидать обслуживания сколь угодно долго. Отметим, что увеличение нагрузки может быть обусловлено двумя факторами: увеличением интенсивности поступления заявок в систему или увеличением длительности обслуживания заявок (например, в результате уменьшения скорости работы обслуживающего прибора).
2. Среднее время ожидания заявок существенно зависит от нагрузки y (загрузки ρ) системы (рис.4.2). При y ≥ 1 (ρ → 1) время ожидания заявок возрастает неограниченно: w → ∞, т.е. заявки могут ожидать обслуживания сколь угодно долго. Отметим, что увеличение нагрузки может быть обусловлено двумя факторами: увеличением интенсивности поступления заявок в систему или увеличением длительности обслуживания заявок (например, в результате уменьшения скорости работы обслуживающего прибора).
3. Можно показать, что для бесприоритетных дисциплин обслуживания в обратном порядке (ООП) и обслуживания в случайном порядке (ОСП) средние времена ожидания заявок будут такими же, как и при обслуживании в порядке поступления, но дисперсии времени ожидания будут больше. Это обусловлено, в частности для дисциплины ООП, тем, что часть заявок, поступивших последними, будут ожидать незначительное время, в то время как заявки, попавшие в начало очереди, могут ожидать обслуживания достаточно долго, то есть увеличивается разброс значений времени ожидания относительно среднего значения.