
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Переведення цілих чисел з однієї системи числення в іншу
|
|
Лабораторна робота № 1
Мета роботи: Ознайомитися зі структурою машинних форматів представлення даних цілочисельного типу та принципами перетворення даних різних форматів.
Теоретичні відомості.
Число в однорідних системах може бути представлено поліномом виду
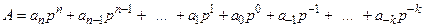 (1.1)
(1.1)
або 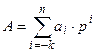 , причому
, причому 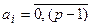 , а знаменник геометричної прогресії р називається основою системи числення. Очевидно, що основою однорідної позиційної системи може бути будь-яке ціле число, оскільки не накладено ніяких обмежень на величину основи. Однорідність системи числення означає, що у всіх розрядах числа, записаного в такій системі, використовують цифри з одної і тієї ж множини. Наприклад, у звичайній десятковій системі числення у всіх розрядах числа використовують цифри з множини 0, 1,...., 9, у двійковій системі - цифри з множини 0, 1, в шістнадцятковій 0,..., 9, A, B, C, D, E, F і т.п.
, а знаменник геометричної прогресії р називається основою системи числення. Очевидно, що основою однорідної позиційної системи може бути будь-яке ціле число, оскільки не накладено ніяких обмежень на величину основи. Однорідність системи числення означає, що у всіх розрядах числа, записаного в такій системі, використовують цифри з одної і тієї ж множини. Наприклад, у звичайній десятковій системі числення у всіх розрядах числа використовують цифри з множини 0, 1,...., 9, у двійковій системі - цифри з множини 0, 1, в шістнадцятковій 0,..., 9, A, B, C, D, E, F і т.п.
У загальному випадку із підстановкою замість q будь-якого числа X може бути представлене у виді полінома від основи q:
Xq = anqn + a n-1qn-1 +...+ a1q1 + aoqo+ a -1q-1, (1.2)
де в якості коефіцієнтів ai можуть стояти будь-які з q цифр, використовуваних у даній системі числення. Співвідношення (1.2) називають розкладанням числа X по ступенях основи системи числення.
Нижче приведена таблиця відповідності між першими 17 позитивними цілими числами для найбільш розповсюджених в обчислювальній техніці систем числення: 10-ої, 2-ий, 8-ий і 16-ий.
Нехай задано число А в довільній системі числення з основою l і його необхідно перевести в нову систему з основою р, тобто перетворити до виду
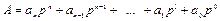 (1.3)
(1.3)
де аі =0÷ (р-1) - база нової системи числення.
Вираз (1.3) можна записати у вигляді А = А1× р + а0 , де 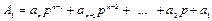 - ціла частина частки; а0 - остача від ділення А на р, яка є цифрою молодшого розряду шуканого числа, записаною у символах старої системи числення.
- ціла частина частки; а0 - остача від ділення А на р, яка є цифрою молодшого розряду шуканого числа, записаною у символах старої системи числення.
Таблица 1.1
| 10-ая | 2-ая | 8-ая | 16-ая |
| A B C D E F |
При діленні числа А1 на р тим же способом отримаємо остачу а1 і т.д. Іншими словами, вираз (1.3) записується по схемі Горнера:
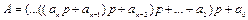 , (1.4)
, (1.4)
після чого його права частина послідовно ділиться на основу нової системи р.
Таким чином, в результаті серії ділень даного числа на основу нової системи числення р знаходимо коефіцієнти
А = А1× р + а0;
А1 = А2× р + а1;
............
Аn-1 = Аn× р + аn-1;
Аn = 0× р + аn;
При цьому ділення продовжується до тих пір, поки не будуть виконані співвідношення: Аn < p; An+1 =0.
Розглянемо правила переведення цілих чисел з однієї системи числення в іншу.
Для переведення цілого числа X10 з системи числення з основою р=10 в систему числення з основою q використовується правило ділення:
1. Число X10 ділиться на нову основу q, представлене в десятковій системі числення.
2. Отримана від ділення перша остача є кількісним еквівалентом молодшї цифри числа з основою q.
3. Частка від ділення знову ділиться на основу q. В результаті одержується нова остача, кількісний еквівалент якої дорівнює наступній цифрі числа з основою q.
4. Ділення відбувається доти, доки не отримається частка менша за дільник. Остання частка дасть кількісний еквівалент старшої цифри числа з основою q.
5. Після завершення ділення перевести кількісні еквіваленти у цифри в q-тій системі числення і записати їх зправа наліво у зворотньому порядку щодо їх одержання.
Приклад 1.
Число 3510 перевести в двійкову систему числення.
Переведення здійснюється за правилом ділення:
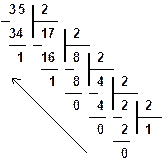
В результаті отримаємо: 3510=1000012.
Приклад 2.
Число 23610 перевести в 16-річну систему числення.
Переведення здійснюється за правилом ділення:
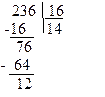
Для переведення довільного числа Xq з системи числення з основою q відмінним від 10 в десяткову систему числення краще користуватися розкладом числа за стпенем основи q (1.2) і виконати дії в 10-ій системі.
Для переведення чисел з системи числення з основою p¹ 10 в систему з основою q¹ 10 можна скористуватися наступною схемою:
Xp® Z10®Yq. (1.5)
Ділення виконувати в двійковій системі числення важко. Тому на практиці при необхідності переведення чисел із системи з малою основою в систему з великою основою зручно користуватись загальним записом чисел у вигляді полінома. В загальному випадку можна обчислити многочлен
А = am× l m +... + a1× l +a0 (1.6)
у вигляді
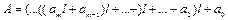 , (1.7)
, (1.7)
представивши в системі з основою р аі і l та виконавши всі дії по правилам арифметики основи р. Наприклад, при переведенні двійкових чисел в десяткову систему числення на практиці підраховують суму степенів основи 2, при яких коефіцієнти аі дорівнюють одиниці. Розрахунки ведуться при цьому в десятковій системі числення.
Завдання на виконання лабораторної роботи.
1) Обрати свій номер варіанта згідно з останньою цифрою у номері залікової книжки (цифра „0” відповідає десятому варіантові).
2) Створити блок-схему алгоритму програми переведення чисел з однієї системи числення в іншу згідно заданого варіанту.
3) Оформити звіт та подати його викладачу разом з результатами виконання роботи.