
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 5. Составить уравнение геометрического места точек, отношение расстояний, которых до данной точки А(4; 0) и до данной прямой x = 1 равно 2.
|
|
Составить уравнение геометрического места точек, отношение расстояний, которых до данной точки А (4; 0) и до данной прямой x = 1 равно 2.
Решение.
В системе координат xOy построим точку А(4; 0) и прямую х = 1.
Пусть М (х; у) – произвольная точка искомого геометрического места точек. Отпустим перпендикуляр МВ на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1, ордината точки В равна ординате точки В. Следовательно, В (1; у)
По условию задачи, МА: МВ = 2. Расстояния МА и МВ находим по формуле
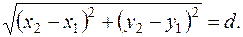
Тогда имеем:
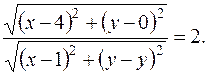
Возведя в квадрат левую и правую части, получим:
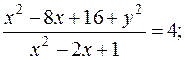
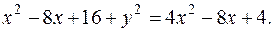
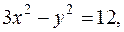 или
или 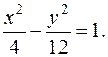
Полученное уравнение представляет собой гиперболу, у которой действительная полуось равна 2, а мнимая равна 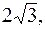 т.е.
т.е.
a = 2, b = 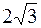 .
.
Определим фокусы гиперболы.
Для гиперболы выполняется равенство c 2 = a 2 + b 2. Следовательно, c 2 = 4 + 12 = 16, с = 4. F 1(– 4; 0), F 2(4; 0) – фокусы гиперболы. Заданная точка А (4; 0) является правым фокусом гиперболы.
Определим эксцентриситет полученной гиперболы:
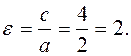
Уравнение асимптот гиперболы имеет вид  и
и 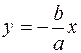 . Следовательно,
. Следовательно, 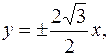 или
или 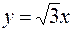 ,
, 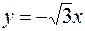 – асимптоты гиперболы.
– асимптоты гиперболы.
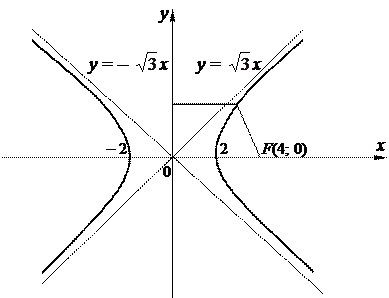
Рисунок 2