
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Переведення дробових чисел з однієї системи числення в іншу. Способи внутрішнього представлення чисел з фіксованою крапкою
|
|
Лабораторна робота № 2
Мета роботи: Ознайомитися з методами переведення правильних дробів з однієї системи числення в іншу та зі структурою машинних форматів чисел з фіксованою крапкою.
Теоретичні відомості. Для представлення дробових даних в ЕОМ необхідно організувати цикл із множенням на 2. При цьому чергова виділена цифра цілої частини може бути або 0, або 1. Такі дії повторюються у циклі доти, доки не буде досягнуто потрібної точності (кількості значущих цифр). Таким чином, необхідно спочатку виділити першу значущу цифру та виділити потрібну кількість цифр, починаючи з першої значущої.
Аналогічно робиться зворотне перетворення з двійкової системи числення у десяткову шляхом множення на 10 у двійковій системі числення. При цьому чергова цифра цілої частини може бути в діапазоні від 0 до 9. Такі дії треба виконувати в циклі по досягненню потрібної точності.
Загальна методика переведення правильних дробів з однієї системи числення в іншу наступна. Нехай правильний дріб А, заданий в довільній позиційній системі числення з основою l, необхідно перевести в нову систему числення р, тобто перетворить до виду
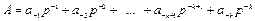 . (2.1)
. (2.1)
Якщо, аналогічно переведенню цілих чисел, розділить обидві частини виразу (2.1) на р-1, тобто помножити на р, то отримаємо А× р = а -1 +А1 , де 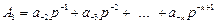 - дробова частина добутку; а -1 - ціла частина результату.
- дробова частина добутку; а -1 - ціла частина результату.
Отримана при цьому цифра цілої частини результату і буде першою цифрою шуканого числа.
Помноживши дробову частину результату А1 знову на р, отримаємо А1× р = а -2 +А2 , де 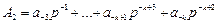 - дробова частина добутку (нового); а -2 - наступна цифра шуканого числа.
- дробова частина добутку (нового); а -2 - наступна цифра шуканого числа.
Звідси слідує, при переведенні вираз (2.1) записується по схемі Горнера
 (2.2)
(2.2)
Перемножуючи його послідовно k раз на основу р, отримаємо шукане число в новій системі числення.
На відміну від цілих чисел, точне переведення можливе не для всіх правильних дробів. Похибка при цьому складає 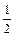 молодшого розряду числа в новій системі.
молодшого розряду числа в новій системі.
Для переведення правильного дробу X10 з десяткової системи числення в систему числення з основою q використовується правило множення:
1. Дане число множиться на нову основу q, представлене в 10-ій системі числення. Ціла частина значення виразу, яка при цьому утворилась, є кількісним еквівалентом першої шуканої цифри числа з основою q.
2. Дробова частина отриманого значення знову множиться на основу q, ціла частина буде кількісним еквівалентом наступної цифри числа з основою q.
3. Множення дробової частини поточного значення на основу q триває доти, доки або дробова частина не стане рівною 0, або не буде знайдений період дробу, або буде досягнута потрібна точність обчислень.
4. Перевести одержані кількісні еквіваленти в цифри в системи числення з основою q за правилом ділення.
Приклад. Перевести задані правильні дроби з десяткової системи числення в систему числення з визначеною основою q:
a) перевести число 0.2510 в число у восьмирічній СЧ:
0.25*8 = 2.00; Таким чином, 0.2510=0.28.
b) перевести число 0.1110 в число у п’ятирічній СЧ:
0.11
х 5 Як видно з обчислень, після чергового
—— множення отримана дробова частина, що
0.55 вже зустрічалася. Тому при наступному
x 5 множенні її на основу 5 буде отримана
—— цифра, що належить періоду дробу.
2.75
x 5 Таким чином, 0.1110=0.02 (3) 5.
——
3.75
c) перевести число 0.3110 в число у двійковій СЧ: 0.31*2=0.62
0.62=0.62*2=1 0.24=0.24*2=0 0.48=0.48*2=0 0.96=0.96*2=1
0.92=0.92*2=...
Зупинемо процес множення, оскільки необхідна точність вже досягнута. Таким чином, 0.3110 ~ 0.010011112.
Переведення дробового числа Xр в число Yq можна здійснити безпосередньо використовуючи правила множення, при цьому нову основу q слід перевести в q'р і виконати множення на це число за правилами системи числення з основою p, а отримані цілі частини добутків після цього перевести в систему з основою q.
Але, як вже зазначалось, виконувати дії в системі числення з основою р¹ 10 досить складно. Тому для переведення правильного дробу з системи числення з основою p¹ 10 в систему з основою q¹ 10 можна користуватися такою схемою:
X p®Z10®Yq.
При поданні чисел у формі з фіксованою крапкою положення крапки фіксується або перед старшим цифровим розрядом (рис.2.1) або після молодшого цифрового розряду (рис. 2.2). У першому випадку можуть бути подані тільки дробові числа за модулем менше 1, у другому - тільки цілі числа.
Традиційно в мікро ЕОМ і мікропроцесорах нумерація розрядів (біт) в розрядній сітці йде справа наліво для цілих чисел і зліва направо для дробових чисел.
Для того щоб комп'ютери могли оперувати з додатними і від'ємними числами, один з розрядів, відводиться під знак числа. Як правило їм є старший (лівий) розряд, при цьому стандартне кодування знаку має вигляд: 0 - для знака " +", 1 - для знака " -".
Знакові числа довжиною n біт подаються в такій формі:
 2-1 2-2 2-3......... 2-(n-2) 2-(n-1) вага розряду
2-1 2-2 2-3......... 2-(n-2) 2-(n-1) вага розряду
| # | # | # | # | … | … | … | # | # |

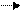 точка фіксована. 0 1 2 3...... n-2 n-1 номер розряду
точка фіксована. 0 1 2 3...... n-2 n-1 номер розряду
 перед старшим
перед старшим 
розрядом знаковий цифрові розряди
розряд
Рис. 2.1
 2n-2 2n-3 ......... 22 21 20 вага розряду
2n-2 2n-3 ......... 22 21 20 вага розряду
| # | # | # | … | … | … | # | # |

 номер разряду n-1 n-2 n-3......... 2 1 0. точка фіксована
номер разряду n-1 n-2 n-3......... 2 1 0. точка фіксована

 після молодшого
після молодшого
знаковий цифрові розряди розряду
розряд
Рис. 2.2
У перших ЕОМ використовувалась форма з фіксованою крапкою перед старшим цифровим розрядом.
Форму з фіксованою крапкою після молодшого розряду використовують, як правило, для подання цілих чисел. При цьому в мікро ЕОМ використовуються два варіанта подання цілих чисел: із знаком і без знака.
Найпростішою формою чисел з фіксованою крапкою після молодшого розряду є форма для подання цілих беззнакових чисел, які мають такий вигляд:
| # | # | # | … | … | … | # | # | # |
 n-1 n-2 n-3......... 2 1 0. номер розряду
n-1 n-2 n-3......... 2 1 0. номер розряду
Рис. 2.3
Цілі без знакові числа при програмуванні використовуються для подання тих числових об'єктів, які принципово не можуть бути від'ємними. Прикладами таких об'єктів є адреси комірок пам'яті, номера рядків програми, лічильники повторень циклів.
Наприклад, при n=16 можна закодувати 2n=65536 адрес комірок пам'яті, якщо врахувати, що комірка пам'яті, як правило, зберігає 1 байт інформації, то така кількість комірок може зберігати 64 Кб закодованої інформації.
Якщо крапка зафіксована після молодшого розряду, то в n-розрядній сітці можна подати нуль, додатні і від'ємні цілі двійкові числа, як правило в діапазоні  .
.
Якщо крапка зафіксована перед старшим розрядом, то в n-розрядній сітці можна подати нуль, додатні і від'ємні правильні дроби у двійковій формі, як правило в діапазоні 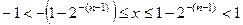 .
.
Використання формату з фіксованою крапкою дозволяє підвищити продуктивність роботи ЕОМ, оскільки операції над такими числами виконуються досить швидко. При цьому в більшості випадків формат чисел з фіксованою крапкою служить для подання цілих двійкових чисел і виконання операцій над ними. Він також є необхідним для виконання операцій " адресної арифметики" над кодами адрес.
Друга частина даної роботи полягає у перетворенні цілих даних з прямого коду у додатковий. Причому формат даних залежить від варіанту.
Як було відзначено, в ЕОМ з метою спрощення виконання арифметичних операцій застосовуються спеціальні коди для представлення чисел. За допомогою цих кодів спрощується визначення знака результату операції, операція вирахування (алгебраїчного додавання – додавання чисел з різними знаками й від’ємних чисел) зводиться до арифметичного додавання кодів, полегшується вироблення ознак переповнення розрядної сітки. Для представлення чисел зі знаком в ЕОМ застосовуються прямий, зворотній і додатковий коди. Загальна ідея побудови коду така. Код трактується як число без знаку, а діапазон чисел, що представляються кодами, без знаку розбивається на два піддіапазони: один з них представляє позитивні числа, а інший - негативні. Розбивка виконується таким чином, щоб приналежність до піддіапазону визначалася максимально просто. Дуже зручно формувати коди так, щоб значення старшого розряду вказувало на знак чисел, що представляються. Використання такого кодування дозволяє говорити про старший розряд як про знаковий, у якому знаходиться 0, якщо число позитивне, і 1, якщо - негативне, а про інших як про цифрові розряди коду, хоча в загальному випадку код трактується як число без знака.
Прямий код. Прямий код цілого двійкового числа X, представленого в n-розрядній сітці визначається так:
X, якщо X > = 0
X пр =
A+¦X¦, якщо X < 0,
де A - величина, рівна вазі старшого розряду сітки, тобто A = 2 n-1 - для цілих чисел і 20=1 – правильних дробів.
Діапазон цілих чисел, що представляються прямим кодом, має вигляд:
-A < X < A.
З визначення випливає, що ненегативні числа представляються кодами (числами без знака) у діапазоні 0 < = Xпр < A, а непозитивні числа -
A < = Xпр < 2A. Так, наприклад, при n=16 маємо:
для ненегативних чисел 0 < = Xпр < = 37767 –діапазон коду,
для непозитивних чисел 37768 < = Xпр < = 65535 – діапазон коду,
діапазон цілих чисел -37767 < = X < = 37767.
Цифрові розряди прямого коду містять модуль числа, що представляється, а знаковий розряд 0 або 1, що забезпечує наочність представлення чисел у прямому коді.
На практиці при побудові прямого коду цілих чисел у знаковий розряд (крайній лівий) заноситься 0, якщо число позитивне і 1, якщо число негативне, а знаковий розряд відокремлюється від цифрових, наприклад, вертикальною рисою |, при цьому усі відсутні старші розряди заповнюються нулями.
Приклад. Представити задані числа в прямому коді, якщо довжина розрядної сітки n дорівнює 8:
a) X = 11101102, тоді Xпр = 0|1110110;
b) X =-101012, тоді Xпр = 1|0010101.
Додавання в прямому коді чисел, що мають однакові знаки виконується досить просто. Числа складаються і сумі привласнюється код знака доданків. Значно більш складною є операція алгебраїчного додавання в цьому коді чисел з різними знаками. У тому випадку приходиться визначати більше по модулю число, робити вирахування модулів чисел і привласнювати різниці знак більшого по модулі числа. Іншим недоліком прямого коду є наявність двох представлень нуля:
позитивний нуль: +0ін = 0|0000...00;
негативний нуль: -0ін = 1|0000...00.
Зазначені недоліки привели до того, що прямий код лише іноді застосовується при введенні і виведенні даних.
Однак операцію вирахування (алгебраїчного додавання) можна звести до операції простого арифметичного додавання за допомогою зворотного і додаткового кодів, використовуваних для представлення в ЕОМ чисел зі знаком. Їхні особливості полягають у тім, що для позитивних чисел вони збігаються з прямим кодом, а для негативних чисел вони є доповненнями деяких чисел.
Зворотний код. Зворотний код двійкового цілого числа X, що представляється в n-розрядній сітці, визначається так
X, якщо X > = 0
Xзв =
B-¦X¦, якщо X < 0,
де B - величина найбільшого числа без знака, що розміщається в n-розрядній сітці, тобто B = 2n –1 – для цілих чисел і B = 2-2-(n-1)– для правильних дробів.
Діапазон чисел, що представляються зворотним кодом, такий же, як і в прямого.
По визначенню зворотний код негативного числа являє собою доповнення модуля вихідного числа до числа B. У зв'язку з цим одержання зворотного коду двійкового негативного числа зводиться до одержання інверсії коду модуля числа, що стоїть в цифрових розрядах.
Для побудови зворотного коду можна користуватися наступним правилом:
1. Побудувати прямий код.
2. Якщо число X - позитивне, то зворотний код отриманий, тобто при X> 0 Xзв = Xпр.
3. Якщо X - негативне число, то в знаковому розряді записати 1, а в цифрових розрядах одиниці замінити нулями, а нулі- одиницями (зробити інверсію).
Приклад. Представити задані числа в зворотному коді, якщо довжина розрядної сітки n=8:
а) X= 111012, тоді Xзв = Xпр = 0|0011101;
b) X=-1000012, тоді Xпр = 1|0100001, Xзв = 1|1011110.
Неважко помітити, що в зворотному коді також існує два представлення нуля: + 0зв = 0|0000...00 і - 0зв = 1|1111...11.
При алгебраїчному додаванні двох двійкових чисел, представлених у зворотному коді, виробляється арифметичне підсумовування цих кодів, включаючи знакові розряди. При виникненні переносу з розряду знака одиниця переносу додається до молодшого розряду суми кодів (такий перенос називається круговим або циклічним). У результаті виходить сума в зворотному коді. Для одержання результату в звичайному виді потрібно скористатися правилом зворотним правилу побудови зворотного коду.
Додатковий код. Основним недоліком алгебраїчного додавання з використанням зворотних кодів складається в наявності циклічного переносу, для чого в процесорі ЕОМ необхідні додаткові витрати часу і схемотехнічні засоби. Від цього недоліку вільний спосіб виконання алгебраїчного додавання в додатковому коді.
Додатковий код двійкового цілого числа X, представленого в n-розрядній сітці, визначається так
X, якщо X > = 0
Xдод =
C-¦X¦, якщо X < 0,
де C - величина, рівна ваги розряду, що випливає за старшим розрядом у n-розрядній сітці, тобто C=2n – для цілих чисел і C=2 – для правильних дробів.
Діапазон чисел, що представляються додатковим кодом, відрізняється від діапазону прямого і зворотного кодів. Так піддіапазони негативних і позитивних чисел різні: для X > = 0 0< = X< A, а для X< 0 0 < ¦X¦ < = A.
Для цілих чисел додатковий код дозволяє використовувати числа в діапазоні -2 n-1< = X < = 2 n-1 -1.
Як видно з визначення, для X> =0 Xпр = Xзв = Xдод.
Для негативних двійкових цілих чисел справедливе співвідношення: Xзв = 2n -1- ¦X¦ = C-¦X¦ - 1, звідси випливає, що Xдод = Xзв + 1.
Таким чином, можна сформулювати наступне правило одержання додаткового коду:
1. Побудувати прямий код числа.
2. Якщо X> =0, то додатковий код побудований, у противному випадку, тобто, якщо X< 0, то потрібно побудувати зворотний код і до молодшого розряду Xзв додати 1.
Приклад. Представити задане число X у додатковому коді, якщо розрядна сітка має довжину n=8:
X = -1001102, оскільки X< 0, то для одержання Xдод виконаємо наступні перетворення:
Xпр = 1|0100110; Xзв = 1|1011001; Xдод = 1|1011001 + 1 = 1|1011010,
таким чином, Xдод = 1|1011010.
Зауваження.
1. На практиці для одержання додаткового коду негативних чисел зручно користуватися наступним простим правилом: записати прямий код числа, потім у цифрових розрядах n-розрядної сітки переглянути всі цифри з права на ліво, зберігши всі молодші нулі і першу що зустрілася 1, а інші розряди інвертувати (див. приклад 7).
2. Одержання числа по його додатковому коді здійснюється в зворотному порядку.
Одним з достоїнств додаткового коду є єдине представлення нуля, дійсно:
+ 0дод = 0|0000...00 і - 0дод = 1|1111...11 + 1

10|0000...00,
оскільки в розрядній сітці представлення числа немає розряду лівіше знакового, тому крайня ліворуч 1 відкидається, а в знаковому розряді буде 0, тобто
- 0дод = 0|0000...00 = + 0дод.
При алгебраїчному додаванні двох двійкових чисел, представлених додатковим кодом, виробляється арифметичне підсумовування цих кодів, включаючи розряди знаків. При виникненні переносу з розряду знака одиниця переносу відкидається (ігнорується). У результаті виходить алгебраїчна сума в додатковому коді.
Завдання на виконання лабораторної роботи.
1) Обрати свій номер варіанта згідно з останньою цифрою у номері залікової книжки (цифра „0” відповідає десятому варіантові).
2) Створити блок-схему алгоритму програми переведення правильних дробів з однієї системи числення в іншу згідно заданого варіанту.
3) Проаналізувати текст паскаль-програми у файлі lab2.pas і визначити її призначення.
4) Скомпілювати програму та запустити на виконання.
5) Підставити власні вхідні значення та проаналізувати результати роботи програми.
6) Оформити звіт та подати його викладачу разом з результатами виконання роботи.