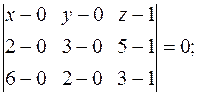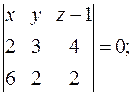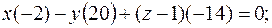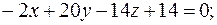Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 4. Даны координаты вершин А(0; 0; 1), В(2; 3; 5), С(6; 2; 3), D(3; 7; 2) пирамиды ABCD
|
|
Даны координаты вершин А (0; 0; 1), В (2; 3; 5), С (6; 2; 3), D (3; 7; 2) пирамиды ABCD. Требуется:
1) записать векторы 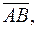
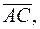
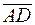 в системе орт
в системе орт 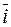 ,
, 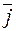 ,
, 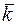 и найти модули этих векторов;
и найти модули этих векторов;
2) найти угол между векторами 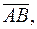
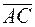 ;
;
3) найти проекцию вектора 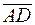 на вектор
на вектор  ;
;
4) найти площадь грани ABC;
5) найти объем пирамиды ABCD;
6) составить уравнение ребра AC;
7) составить уравнение грани ABC.
1. Известно, что произвольный вектор 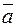 представляется в системе орт
представляется в системе орт 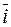 ,
, 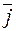 ,
, 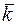 по формуле
по формуле
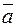 = ax
= ax 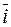 + ay
+ ay 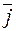 + az
+ az 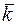 , (1)
, (1)
где ax, ay, az – координаты вектора 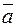 в системе координат, порожденной ортами, причем
в системе координат, порожденной ортами, причем
ax = npOx 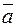 , ay = npOy
, ay = npOy 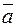 , az = npOz
, az = npOz 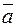 .
.
Если заданы точки M 1(x 1, y 1, z 1), M 2(x 2, y 2, z 2), то для вектора
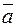 =
= 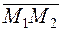 .
.
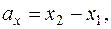
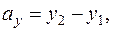
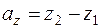 ,
,
то есть
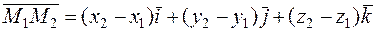 . (2)
. (2)
Воспользовавшись формулой (2) и координатами заданных точек А, В, С, D получим:
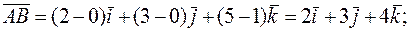

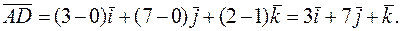
Если вектор 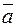 задан формулой (1), то его модуль вычисляется следующим образом:
задан формулой (1), то его модуль вычисляется следующим образом:
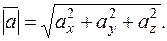 (3)
(3)
Используя формулу (3), получаем модули найденных векторов:
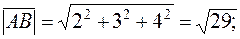
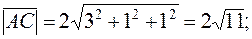
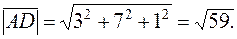
2. Известна формула cos 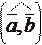 =
= 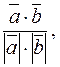 где
где 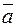 ·
· 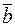 – скалярное произведение векторов
– скалярное произведение векторов 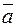 и
и 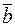 , которое можно вычислить следующим образом:
, которое можно вычислить следующим образом:
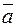 ·
· 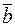 =
= 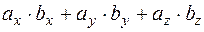 .
.
У нас
cos φ = cos 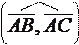 =
= 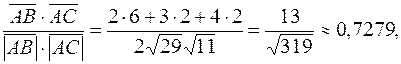
то есть 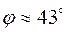 .
.
3. Известно, что
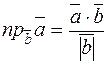 ,
,
то есть в нашем случае
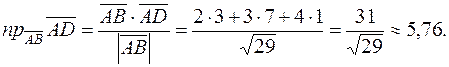
4. Воспользуемся формулой нахождения площади треугольника, построенного на векторах 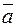 и
и 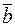 :
:
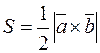 ,
,
где 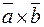 – векторное произведение векторов, которое можно вычислить по следующему правилу:
– векторное произведение векторов, которое можно вычислить по следующему правилу:
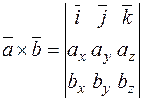 .
.
В нашем примере 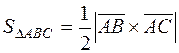 , причем
, причем
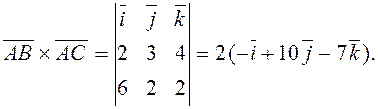
Таким образом,
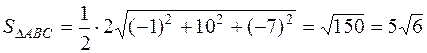 (кв.ед.).
(кв.ед.).
5. Объем пирамиды, построенной на трех некомпланарных векторах 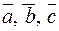 , можно найти по формуле
, можно найти по формуле
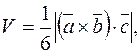
где 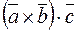 – смешанное произведение векторов, которое вычисляется следующим образом:
– смешанное произведение векторов, которое вычисляется следующим образом:
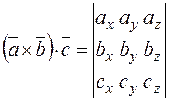 .
.
У нас 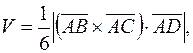 где
где
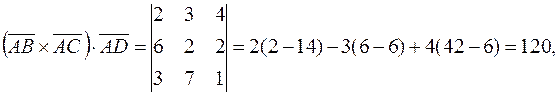
то есть 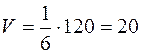 (куб. ед.).
(куб. ед.).
6. Известно, что уравнение прямой, проходящей через две заданные точки пространства 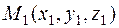 и
и 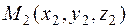 , имеет вид:
, имеет вид:
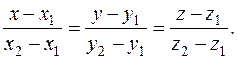 (4)
(4)
Подставив в (4) координаты точек A и C, получим

то есть уравнение ребра AC окончательно запишется следующим
образом:
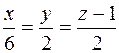 или
или 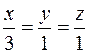 .
.
7. Уравнение плоскости, проходящей через три заданные точки 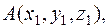
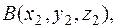
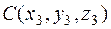 можно записать в виде:
можно записать в виде:
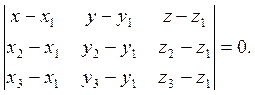
Подставляя в него координаты точек A, B, C, получим