Й способ решения

ЕН. Ф. 01 МАТЕМАТИКА

Методические указания

и варианты заданий к контрольной работе № 1

для всех направлений бакалавриата

Уфа 2014

УДК 51(07)

ББК 22.1я73, 22.161.6

М 54

Рекомендовано к изданию методической комиссией факультета лесного хозяйства (протокол № 6 от 3 марта 2014 года и заседанием кафедры математики (протокол № 6 от 27 февраля 2014 года)

Составители: доцент, к.соц.н. Саитова Р.З.

доцент, к.физ.-мат.н. Маннанов М.М.

Рецензент: доцент кафедры физики Юмагужин Р.Ю.

Ответственный за выпуск: зав. кафедрой математики

доцент, к.физ.-мат.н. Лукманов Р.Л.

ВВЕДЕНИЕ

Целью настоящих методических указаний является помощь студентам в освоении и закреплении следующих разделов математики: линейная и векторная алгебра, аналитическая геометрия.

Расчетно-графическая работа № 1 состоит из 5 заданий. В каждом задании 30 вариантов. Номер варианта студент выбирает по формуле: № = a · b + c, где a – номер задания, b и с – предпоследняя и последняя цифры шифра (номера зачетной книжки или студенческого билета).

Например, номер студенческого билета (зачетки) студента 1265. Тогда в первом задании этот студент выполняет вариант:
№ = 1 · 6 + 5 = 11. Во втором задании: № = 2 · 6 + 5 = 17 и т.д. Если получается вариант больше 30, то нужно вычитать 30. Например, для этого же студента третье задание будет высчитываться: 5 · 6 + 5 = 35. Следовательно, этот студент решает 35 – 30 = 5 – пятый вариант третьего задания.

Прежде чем приступать к выполнению работы, целесообразно изучить соответствующие разделы в учебниках, рекомендованных в библиографическом списке.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1

й способ решения

Пусть требуется, используя формулы Крамера, решить систему

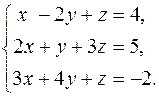
Подсчитаем сначала главный определитель системы ∆, воспользовавшись следующим правилом вычисления определителей третьего порядка:

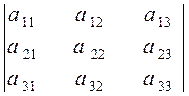= а ₁₁ · – а ₁₂ · 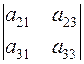+ а ₁₃ · .

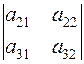У нас ∆ = 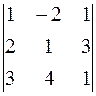= 1 ∙ (1 – 12) + 2 ∙ (2 – 9) + 1 ∙ (8 – 3) = – 20.

Так как ∆ ≠ 0, делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители ∆ x, ∆ y, ∆ z:

∆ x = 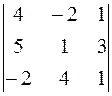= 4 · (1 – 12) – (– 2) · (5 + 6) + 1 · (20 + 2) = 0,

∆ y = 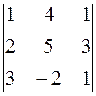= 1 · (5 + 6) – 4 · (2 – 9) + 1 · (– 4 – 15) = 20,

∆ z = 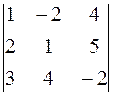= 1 · (– 2 – 20) – (– 2) · (– 4 – 15) + 4 · (8 – 3) = – 40.

Далее, воспользовавшись формулами Крамера, окончательно получим

x = 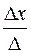= 0, y = 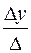= – 1, z = 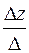= 2.

Всем трем равенствам они удовлетворяют, поэтому делаем вывод о правильности полученного решения: x = 0; y = – 1; z = 2.