Определенный интеграл

Лекция № 15.

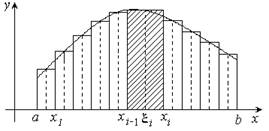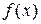Пусть на отрезке задана функция . Разобьем отрезок точками 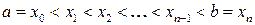на 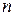элементарных отрезков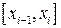 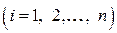длины 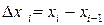. В каждом из этих отрезков 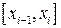возьмем произвольную точку 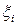и составим сумму 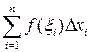, называемую интегральной суммой (Римана) для функции 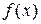на отрезке .

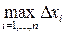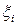Определение 37.1. Пусть предел последовательности интегральных сумм при стремлении к нулю существует, конечен и не зависит ни от способа разбиения отрезка , ни от выбора точек . Этот предел называется определенным интегралом от функции 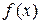на отрезке и обозначается

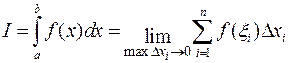(1)

При этом число называется нижним пределом, число 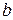– его верхним пределом; функция 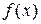– подынтегральной функцией, выражение 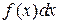– подынтегральным выражением, а задача о нахождении 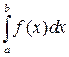– интегрированием функции 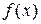на отрезке .

Все непрерывные на отрезке функции интегрируемы на этом отрезке. Интегрируемыми будут и ограниченные функции, имеющие на конечное число точек разрыва.