
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определенный интеграл как функция верхнего предела
|
|
Ранее, строя новые функции из известных, мы использовали четыре арифметических действия и суперпозицию функций. Сейчас мы рассмотрим принципиально иной способ построения новых функций из известных.
Если 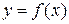 интегрируема на отрезке
интегрируема на отрезке  , то, очевидно, она интегрируема также на любом отрезке
, то, очевидно, она интегрируема также на любом отрезке 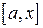 , вложенном в
, вложенном в  .
.
Положим по определению
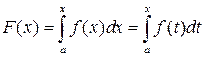 ,
,
где 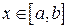 , а функция
, а функция 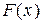 называется интегралом с переменным верхним пределом.
называется интегралом с переменным верхним пределом.
Пусть 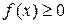 на отрезке
на отрезке  . Тогда значение функции
. Тогда значение функции 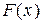 в точке
в точке 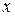 равно площади
равно площади 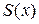 под кривой
под кривой 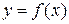 на отрезке
на отрезке 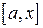 .
.
Это позволяет по новому взглянуть на некоторые известные функцию Например,  , где
, где 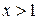 , поэтому значение функции
, поэтому значение функции 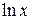 в точке
в точке 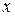 численно равно площади
численно равно площади 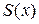 под гиперболой
под гиперболой 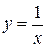 на отрезке
на отрезке 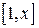 .
.
Рассмотрим теперь свойства функции 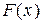 .
.
Теорема 1. Пусть функция 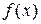 непрерывна на отрезке
непрерывна на отрезке  . Тогда в каждой точке
. Тогда в каждой точке 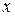 отрезка
отрезка  производная функции
производная функции 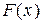 по переменному верхнему пределу равна подынтегральной функции
по переменному верхнему пределу равна подынтегральной функции 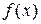 , т.е.
, т.е.
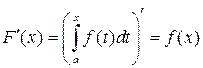 . (2)
. (2)
Доказательство.
Покажем, что функция
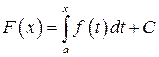 (3)
(3)
является первообразной функции 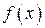 .
.
Согласно определению производной,
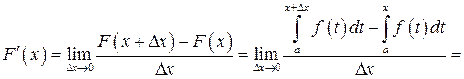
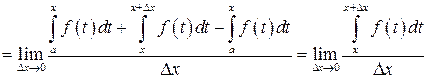 .
.
Применяя теорему о среднем к промежутку  , представим интеграл в числителе в виде
, представим интеграл в числителе в виде 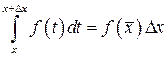 , где
, где 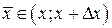 и
и 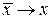 при
при 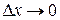 .
.
Следовательно, 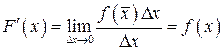 .
.
Теорема 2. Если функция 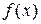 непрерывна на отрезке
непрерывна на отрезке  , то функция
, то функция 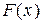 также непрерывна на
также непрерывна на  .
.
Вычисление определенного интеграла возможно с применением первообразной для функции 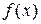 по формуле Ньютона-Лейбница.
по формуле Ньютона-Лейбница.
Теорема 3. Если функция 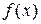 непрерывна на отрезке
непрерывна на отрезке  и
и 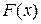 – первообразная функции
– первообразная функции 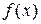 , то
, то
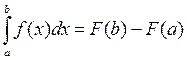 . (4)
. (4)
Формула (4) называется формулой Ньютона–Лейбница.
Доказательство.
Возвратимся к уравнению (3). Полагая 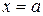 , находим значение постоянной
, находим значение постоянной 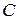 :
:
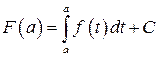
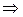
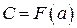 .
.
Полагая в этом же уравнении 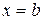 , получаем:
, получаем:
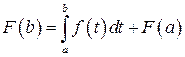
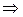
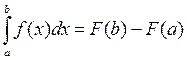 .
.
Нахождение определённых интегралов с использованием формулы (4) осуществляется в два шага: на первом шаге находят первообразную 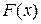 для подынтегральной функции
для подынтегральной функции 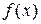 ; на втором – применяется собственно формула (3) – находится приращение первообразной, равное искомому интегралу. Введем обозначение для приращения первообразной
; на втором – применяется собственно формула (3) – находится приращение первообразной, равное искомому интегралу. Введем обозначение для приращения первообразной
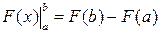 .
.
Все методы, применяемые при вычислении первообразной, переносятся на вычисление определенного интеграла.
Теорема 4. (замена переменной в определённом интеграле). Если выполнены условия:
1) функция 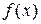 непрерывна на отрезке
непрерывна на отрезке  ;
;
2) отрезок  является множеством значений функции
является множеством значений функции 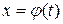 , определенной на отрезке
, определенной на отрезке 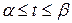 и имеющей на нем непрерывную производную;
и имеющей на нем непрерывную производную;
3) 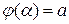 и
и 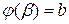 , то справедлива формула
, то справедлива формула
.
Пример 1. Вычислить 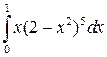 .
.
Решение. Положим 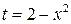 . Тогда
. Тогда 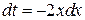 и
и 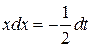 .
.
Если 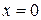 , то
, то 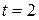 , и если
, и если 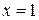 , то
, то 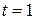 . Следовательно,
. Следовательно,
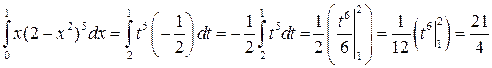 .
.
Формула замены переменной для определённого интеграла даже удобнее, чем для неопределённого. Нам не нужно возвращаться к исходным переменным, а вместо этого нужно поменять пределы интегрирования.
Рассмотрим, как выполняется интегрирование по частям в определённом интеграле.
Теорема 5. Если функции 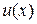 и
и 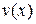 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  , то справедлива формула
, то справедлива формула
.
Пример 2. Вычислить 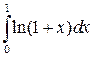 .
.