Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур.Если непрерывная кривая задана в прямоугольных координатах уравнением

Вычисление площадей плоских фигур. Если непрерывная кривая задана в прямоугольных координатах уравнением 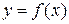, где 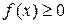на отрезке , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикалями 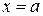; 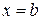и отрезком оси абсцисс 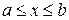, вычисляется по формуле

.

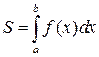Пример 3. Вычислить площадь, ограниченную параболой 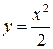, прямыми 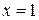, 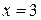и осью абсцисс.

Решение.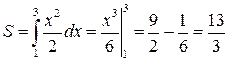

Пример 4. Вычислить площадь, ограниченную кривой 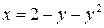и осью ординат.

Решение. Здесь изменены роли осей координат, поэтому искомая площадь будет выражаться интегралом

.

В общем случае, если площадь 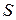ограничена двумя непрерывными кривыми 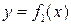; 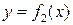и двумя вертикалями 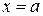; 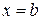, где 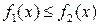, для вычисления площади фигуры имеем формулу

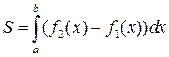
Пример 5. Вычислить площадь 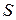, заключенную между кривым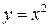и и .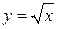

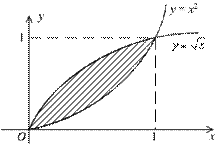Решение. Найдем точки пересечения кривых: 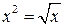, , 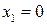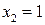. На отрезке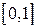 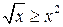. Значит,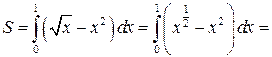

.
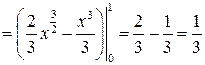