Динамическое торможение

Якорная обмотка двигателя отключается от источника питания сети и замыкается на тормозное сопротивление, т.е.:

,

,

.

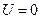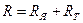При сохранении потока, момент 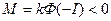, и по отношению к направлению скорости момент становится тормозным, и рабочая точка перемещается из 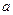в 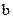. Под действием тормозного момента 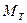двигатель замедляется и останавливается:

,

,

,

.

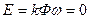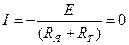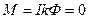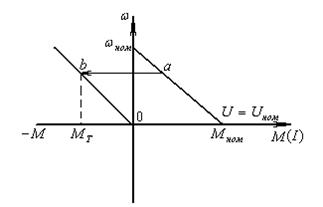
Рис.24 Механическая характеристика ДПТ с НВ при динамическом торможении

Главное достоинство динамического торможения - точная остановка двигателя (при , ).

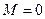Уравнение механической характеристики:

.

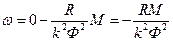Наклон механической характеристики зависит от величины тормозного сопротивления, которое вводится для ограничения тока 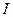якоря и предотвращения перегрева двигателя.

,

.

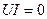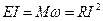Т.о. вся механическая энергия, потребляемая двигателем от механизма, рассеивается в виде тепла в двигателе:

.

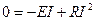2.2.4 ДПТ с НВ, как объект управления. Динамическая модель ДПТ с НВ в переменных «входы-выходы». Аналоговый вариант

Задача: представить динамическую модель ДПТ с НВ в переменных «входы-выходы» в виде структурной схемы. Для этого представим систему уравнений, описывающих электромагнитные и динамические процессы, происходящие в ДПТ с НВ.

Уравнение магнитного потока возбуждения:

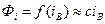. (19)

Уравнение равновесия обмотки возбуждения:

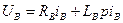, (20)

где 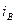- ток обмотки возбуждения;

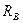- активное сопротивление обмотки возбуждения;

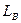- индуктивность обмотки возбуждения;

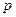- оператор дифференцирования;

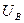- напряжение, приложенное к обмотке возбуждения.

Уравнение равновесия обмотки якоря:

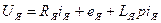(21)

Уравнение ЭДС в обмотке якоря:

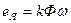(22)

Конструкционная постоянная машины :

,

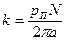где 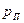- число пар полюсов;

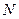- число активных проводников;

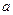- число параллельных ветвей.

Уравнение электромагнитного момента:

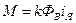(23)

Уравнения (19) - (23) соответствуют определению математической модели (описанию) ДПТ с НВ. Определение параметров в уравнении (19) - (23) по паспортным данным двигателя рассмотрены в курсе ЭП.

Индуктивность якорной цепи можно грубо определить:

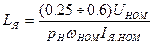
В этом уравнении коэффициент 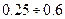выбирается исходя из их номинальной мощности. Так, например, у двигателя мощностью 200 кВт этот коэффициент 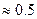, с увеличением мощности коэффициент увеличивается. Для определения параметров в цепи возбуждения - тока и сопротивления обмотки возбуждения, 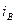и 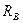соответственно, обычно требуются сведения, не сообщающиеся в общедоступных каналах, такие как число витков, соединение обмоток полюсов. Чаще всего для этих целей используют кривые намагничивания, которые характеризуют материал, из которого изготовлен сердечник статора.

Для более грубой оценки пользуются постоянной времени обмотки возбуждения:

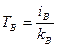
Рис. 25а Кривая намагничивания

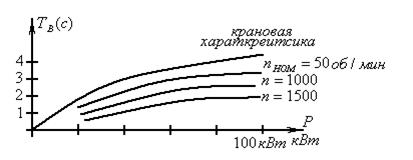
Рис.25б Зависимость постоянной времени ОВ от мощности

Чаще, в соответствии с принципом поставленных задач, принято считать, что в процессе работы привода изменения вносятся либо в обмотку возбуждения, либо в обмотку якоря. В этом случае задача по совместному решению уравнений (19) - (23) значительно упрощаются.

Представим динамическую модель ДПТ с НВ в виде структурной схемы в переменных «входы-выходы», при , и 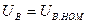, выбрав в качестве входных переменных 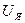и .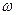

Тогда:

,

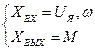
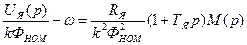где , ,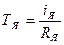

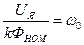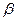- статическая жесткость,

.

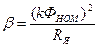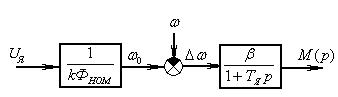
Рис. 26 Структурная схема динамической модели ДПТ с НВ