Выборочная дисперсия.

Смещенной оценкой генеральной дисперсии служит выборочная дисперсия. Эту величину вводят для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг среднего значения .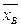

Определение. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если значения признака x₁, x₂, …, x_k имеют соответственно частоты n₁, n₂, …, n_k, причем n₁ + n₂ + … + n_k = n, то

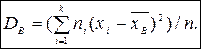
Эта оценка является смещенной, так как ,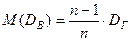

где D_Г – генеральная дисперсия – среднее арифметическое квадратов отклонения значения признака генеральной совокупности от их среднего значения .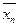

Теорема. Выборочная дисперсия равна среднему квадратов значений признака минус квадрат выборочной средней.

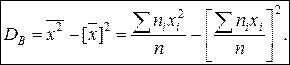
Для вычисления выборочной дисперсии эта формула наиболее удобна.

Замечание. Если перейти к условным вариантам u_i = x_i – c, то дисперсия при этом не изменится. Тогда .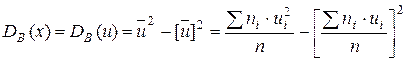

Оценка генеральной дисперсии по исправленной выборочной.

Пусть из генеральной совокупности в результате n независимых наблюдений

над количественным признаком Х извлечена повторная выборка объема n:

При этом n₁ + n₂ + … + n_k = n. Требуется по данным выборки найти неизвестную генеральную дисперсию D_Г. Если в качестве оценки D_Г принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение D_Г. Объясняется это тем, что математическое ожидание выборочной дисперсии не равно оцениваемой D_Г, а равно .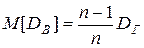

Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить 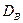на дробь n/(n–1). Сделав это, мы получим исправленную дисперсию, которую обычно обозначают .

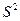Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:

.

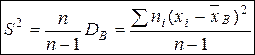Более удобна форма:

.

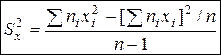В условных вариантах она имеет вид:

,

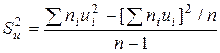причем если u_i = x_i – c, то 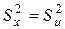; если 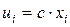, то .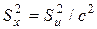

Задача 1.

Из генеральной совокупности извлечена выборка объемом n = 60

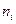
Найти несмещенную оценку генеральной средней.

Решение. Несмещенной оценкой генеральной средней является выборочная средняя: ,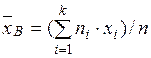

где 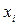─ варианта выборки, 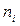─ частота варианты 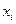; 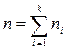объем выборки.

.

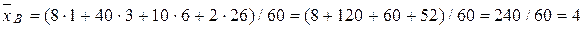Ответ: .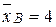

Задача 2.