Элементы теории корреляции

Определение. Зависимость двухслучайных величин называют корреляционной, если изменение одной случайной величины приводит к

изменению среднего значения другой случайной величины.

Основные задачи теории корреляции:

1. определить есть ли связь между случайными величинами, если есть, то найти уравнение зависимости (уравнение регрессии);

2. определить силу (тесноту) связи между случайными величинами.

Для определения самого факта связи между случайными величинами и тесноты связи служит коэффициент корреляции. Уравнение регрессии позволяет предсказать, какие изменения в среднем будет претерпевать признак при изменении другого признака.

Если уравнения регрессии являются линейными, то есть графиками будут прямые линии, то корреляционная зависимость называется линейной.

Выборочный коэффициент корреляции 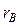находится по формуле:

.

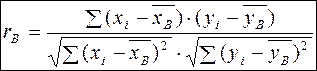Свойства выборочного коэффициента корреляции:

1. Значения коэффициента корреляции изменяются на отрезке [–1; 1]:

.

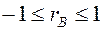2. Чем модуль 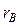больше и ближе к 1, тем теснее связь между изучаемыми признаками.

3. Если 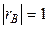, то между признаками функциональная связь.

4. Если 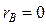, то между изучаемыми признаками нет линейной корреляционной зависимости.

5. Если 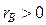, то между признаками прямая (положительная) связь, если 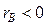, то между признаками обратная (отрицательная) связь.

Выборочное уравнение прямой регрессии Y на X имеет вид:

,

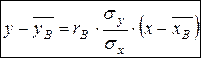где , – выборочные средние, за приближенные значения σ _y и σ _x принимают соответственно s_x и s_y:

, .

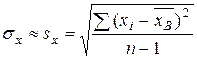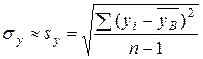Выборочное уравнение прямой регрессии X на Y имеет вид:

,

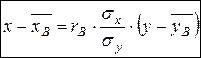Пример. Были произведены измерения общей длины ствола в см (X) и длины его части без ветвей (Y) 10 молодых сосен. Результаты этого измерения представлены в таблице:

Вычислить выборочный коэффициент корреляции и найти выборочное уравнение прямой регрессии Y на X.

Решение. Вычислим выборочный коэффициент корреляции по формуле:

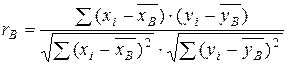
Для вычисления величин, входящих в формулу, составим вспомогательную таблицу (приведена на следующей странице), в которой результаты измерений записаны столбцами. Внизу каждого из столбцов вычислены суммы для нахождения средних 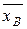и 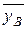. Далее расположены столбцы, в которых вычисляются разности x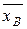_i– и yi– 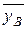, их квадраты и произведения. Значения этих столбцов суммируются (последняя строка), чтобы получились величины, необходимые для подстановки в формулу. Отметим, что суммы в столбцах, в которых вычислены разности x_i– 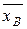и

y_i– 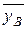будут всегда равны нулю.

Находим средние 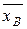и 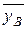(смотри данные в таблице, 1–2 столбцы):

= 700/10 = 70, = 230/10 = 23.

Выполнив все вычисления в таблице (3 – 7 столбцы), получаем:

Σ (x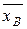_i– )(y_i– 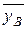) =1520,

Σ (x_i– 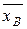)² = 8250,

Σ (y_i– 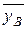)² = 298.

Подставляя эти значения в соответствующую формулу, вычислим коэффициент корреляции:

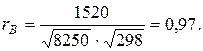
xi	yi	xi–	(xi– )2	yi–	(yi– )2	(xi– )(yi– )
		–45 –35 –25 –15 –5		–9 –5 –4 –3

Таким образом, у выбранных сосен имеет место очень сильная корреляция между общей длиной ствола и длиной его части без ветвей.

Найдем теперь выборочное уравнение прямой регрессии Y на X.

,

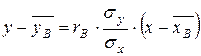где , .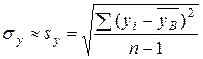

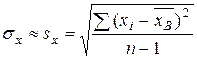Тогда σ _y/σ _x=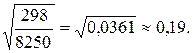

Подставляя в выборочное уравнение прямой регрессии Y на X: 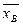=70, 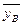=23, r_B=0, 97, σ _y/σ _x=0, 19, получим y–23=0, 97∙ 0, 19∙ (x–70) или y–23=0, 18x–12, 6.

Окончательно, y=0, 18x + 10, 4 – искомое уравнение прямой регрессии Y на X.