
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение типовых задач по математической статистике
|
|
Задача 1. Из крупного стада коров произведена случайная выборка, получено 20 вариант удоя коров за 300 дней лактации (в ц): 35, 9; 35, 3; 42, 7; 45, 2; 25, 9; 35, 5; 33, 4; 27, 0; 35, 9; 38, 8; 33, 7; 38, 6; 40, 9; 35, 5; 44, 1; 37, 4; 34, 2; 30, 8; 38, 4; 31, 3.
Требуется получить вариационный ряд и построить гистограмму относительных частот; найти основные выборочные характеристики: 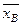 , s2, s, V, sx; с надежностью 95% указать доверительный интервал для оценки генеральной средней xГ.
, s2, s, V, sx; с надежностью 95% указать доверительный интервал для оценки генеральной средней xГ.
Решение. Запишем исходные данные в виде вариационного ряда, то есть располагая их в порядке возрастания: 25, 9; 27, 0; 30, 8; 31, 3; 33, 4; 33, 7: 34, 2; 35, 3; 35, 3; 35, 5; 35, 9; 35, 9; 37, 4; 38, 4; 38, 6; 38, 8; 40, 9; 42, 7; 44, 1; 46, 2.
Максимальное значение признака составляет 46, 2 ц, а минимальное – 25, 9 ц. Разница между ними составляет 20, 3 ц. Этот интервал надо разбить на определенное количество классов. При малом объеме выборки (20–40 вариант) намечают 5–6 классов. Возьмем длину интервала ∆ x=5. Получаем пять интервалов: первый 25 – 30, второй 30 – 35, третий 35 – 40, четвертый 40 – 45, пятый 45 – 50. С помощью ранжированного ряда определим частоту попадания вариант выборки в каждый интервал. В первый интервал попадет два значения, поэтому n1= 2. Во второй интервал попадают пять значений, поэтому n2= 5. Аналогично n3= 9, n4=3, n5= 1.
Теперь найдем относительные частоты попадания вариант выборки в каждый интервал:
w1=n1/n=2/20=0, 1; w2=n2/n=5/20=0, 25; w3=n3/n=9/20=0, 45;
w4=n4/n=3/20=0, 15; w5=n5/n=1/20=0, 05.
Для проверки вычисляем сумму относительных частот:
w1+ w2+ w3+ w4+ w5=0, 1+0, 25+0, 45+0, 15+0, 05=1.
Тот факт, что в сумме получена единица, подтверждает правильность вычислений.
Вычислим плотности wi/∆ x относительных частот вариант. Получаем
w1/∆ x1=0, 1/5=0, 02; w2/∆ x2=0, 25/5=0, 05; w3/∆ x3=0, 45/5=0, 09;
w4/∆ x4=0, 15/5=0, 03; w5/∆ x5=0, 05/5=0, 01.
Полученные результаты сведем в таблицу.
| Интервал значений | 25–30 | 30–35 | 35–40 | 40–45 | 45–50 |
| Частоты вариант | |||||
| Относительные частоты | 0, 10 | 0, 25 | 0, 45 | 0, 15 | 0, 05 |
| Плотность относительных частот | 0, 02 | 0, 05 | 0, 09 | 0, 03 | 0, 01 |
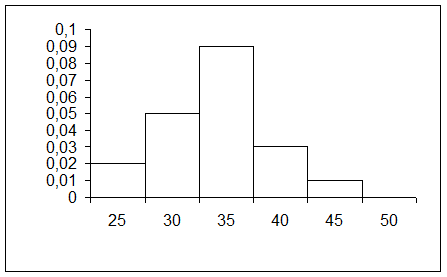
Строим гистограмму относительных частот – ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются интервалы, а высотами соответствующие значения плотностей относительных частот.
Основные выборочные характеристики вычисляются по формулам: 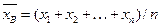 – выборочная средняя;
– выборочная средняя;  – «исправленная» дисперсия;
– «исправленная» дисперсия; 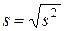 – среднее квадратическое отклонение;
– среднее квадратическое отклонение; 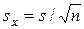 – ошибка средней;
– ошибка средней; 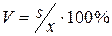 – коэффициент вариации.
– коэффициент вариации.
Расчеты удобно проводить с помощью таблицы
| № | Результат обследования xi | xi– 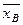
| (xi– 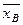 )2 )2
|
| 35, 9 | –0, 1 | 0, 01 | |
| 35, 3 | –0, 7 | 0, 49 | |
| 42, 7 | 6, 7 | 44, 89 | |
| 45, 2 | 9, 2 | 84, 64 | |
| 25, 9 | –10, 1 | 102, 01 | |
| 35, 3 | –0, 7 | 0, 49 | |
| 33, 4 | –2, 6 | 6, 76 | |
| 27, 0 | –9, 0 | 81, 00 | |
| 35, 9 | –0, 1 | 0, 01 | |
| 38, 8 | 2, 8 | 7, 84 | |
| 33, 7 | –2, 3 | 5, 29 | |
| 38, 6 | 2, 6 | 6, 76 | |
| 40, 9 | 4, 9 | 24, 01 | |
| 35, 5 | –0, 5 | 0, 25 | |
| 44, 1 | 8, 1 | 65, 61 | |
| 37, 4 | 1, 4 | 1, 86 | |
| 34, 2 | –1, 8 | 3, 24 | |
| 30, 8 | –5, 2 | 27, 04 | |
| 38, 4 | 2, 4 | 5, 76 | |
| 31, 3 | –4, 7 | 22, 09 | |
| Σ | 720, 3 | 490, 05 |
Подставляя полученные значения в формулы, получаем
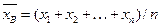 = 720, 3/20 = 36, 015;
= 720, 3/20 = 36, 015;
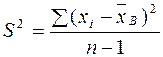 = 490, 05/19 = 25, 79;
= 490, 05/19 = 25, 79;
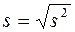 = 5, 08;
= 5, 08;
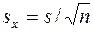 = 5, 08/4, 47 = 1, 34;
= 5, 08/4, 47 = 1, 34;
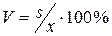 = 5, 08/36∙ 100% = 14%.
= 5, 08/36∙ 100% = 14%.
Доверительный интервал для оценки генеральной средней имеет вид:
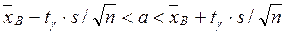 .
.
Вычисляем теперь радиус доверительного интервала:
tγ ∙ sx = 2, 10ּ 1, 34 = 2, 8,
где значение 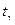 = 2, 10 находим по таблице приложения 3.
= 2, 10 находим по таблице приложения 3.
Таким образом, с надежностью 95% можно утверждать, что во всем стаде средний удой за 300 дней заключен в пределах от  = 36 – 2, 8 = =33, 2 ц (гарантированный минимум) до
= 36 – 2, 8 = =33, 2 ц (гарантированный минимум) до 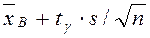 = 36 + 2, 08 = 38, 8 ц (возможный максимум).
= 36 + 2, 08 = 38, 8 ц (возможный максимум).
Задача 2. Для определения средней урожайности сахарной свеклы в колхозе на площади 1000 га была определена ее урожайность на 100 га. Результаты выборочного обследования представлены следующим распределением:
| Урожайность, ц/га | 23–25 | 25–27 | 27–29 | 29–31 | 31–33 | 33–35 | 35–37 |
| Площадь, га |
Найти величину, которую следует принять за среднюю урожайность на всем массиве; величину, которую следует принять за среднее квадратическое отклонение урожайности на всем массиве; доверительный интервал, в котором с вероятностью 0, 95 заключена средняя урожайность на всем массиве.
Решение. В качестве приближенного значения средней урожайности на всем массиве принимаем среднюю арифметическую данного распределения, то есть выборочную среднюю. За значение признака нужно принять середины интервалов. Получим:
(24∙ 3+2∙ 10+28∙ 6+30 ∙ 16+3 ∙ 15+34∙ 30+36∙ 20)/100 = 3200/100 = 32.
Для оценки дисперсии генеральной совокупности применяем формулу
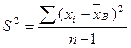 =1/99ּ (3∙ (24–32)2+10∙ (26–32)2+6∙ (28–32)2+
=1/99ּ (3∙ (24–32)2+10∙ (26–32)2+6∙ (28–32)2+
+16∙ (30–32)2+15∙ (32–32)2+30∙ (34–32)2+20∙ (36–32)2)= =1/99ּ (192+360+96+64+0+120+320)=1/99ּ 1152=11, 64.
Отсюда можно найти среднее квадратическое отклонение урожайности на всем массиве  =
= 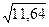 = 3, 4.
= 3, 4.
Найдем среднее квадратическое отклонение выборочной средней по формуле
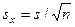 = 3, 4/
= 3, 4/ 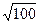 = 0, 34 ц.
= 0, 34 ц.
Итак, оценка средней урожайности сахарной свеклы на всем массиве равна 32 ц со средней квадратической ошибкой 0, 34 ц. Оценка среднего квадратического отклонения урожайности на всем массиве равна 3, 4 ц.
Для вычисления доверительного интервала воспользуемся равенством
P(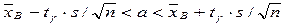 ) = γ,
) = γ,
согласно которому можно утверждать, что с надежностью γ доверительный интервал 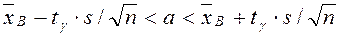 покрывает неизвестное математическое ожидание, точность оценки
покрывает неизвестное математическое ожидание, точность оценки 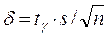 .
.
Так как n = 100 > 30, то значениеtγ найдем из условия γ =2Ф(tγ )=0, 95. По таблице приложения 2 находим значение Ф(tγ )=0, 475 и tγ =1, 96.
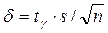 = 1, 96ּ 3, 4/
= 1, 96ּ 3, 4/ 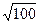 = 0, 67.
= 0, 67.
Концы доверительного интервала:
 = 32 – 0, 67 = 31, 33 и
= 32 – 0, 67 = 31, 33 и 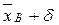 = 32 + 0, 67 = 32, 67.
= 32 + 0, 67 = 32, 67.
Таким образом, с вероятностью 0, 95 средняя урожайность сахарной свеклы на всем массиве заключена в границах от 31, 33 ц до 32, 67 ц.