Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Түзудің канондық теңдеуі
|
|
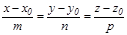
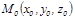 нү ктесі тү зудің бойында жатсын жә не ол тү зу
нү ктесі тү зудің бойында жатсын жә не ол тү зу 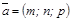 векторына параллель болсын. Тү зудің бойынан кез келген
векторына параллель болсын. Тү зудің бойынан кез келген 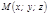 нү ктесін аламыз. Сонда,
нү ктесін аламыз. Сонда, 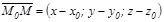 .
. 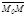 векторы тү зудің бойында жатқ андық тан
векторы тү зудің бойында жатқ андық тан 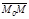 ||
|| 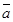 болады. Сондық тан тү зудің канондық тең деуі:
болады. Сондық тан тү зудің канондық тең деуі:
 (5.8)
(5.8)
Мұ ндағ ы 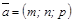 - бағ ыттаушы вектор деп аталады.
- бағ ыттаушы вектор деп аталады.
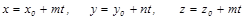 3. Тү зудің параметрлік тең деуі. (5.7) тең деуіндегі ә р тең дікті
3. Тү зудің параметрлік тең деуі. (5.7) тең деуіндегі ә р тең дікті 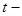 ғ а тең еп, мына тең деуді аламыз:
ғ а тең еп, мына тең деуді аламыз:
(5.9)
4. Тү зудің жалпы тең деуі. Ө зара параллель емес екі жазық тық жалпы тең деулерімен берілсін:
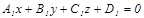 ,
,
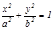 Сонда бұ л жазық тық тар бір тү зудің бойымен қ иылысады. Ендеше осы екі жазық тық тың қ иылысқ ан тү зуінің бойындағ ы кез келген нү ктенің координаттары екі жазық тық тың да тең деуін қ анағ аттандырады. Сондық тан осы екі тең деулер жү йесін тү зудің жалпы тең деуі дейді.
Сонда бұ л жазық тық тар бір тү зудің бойымен қ иылысады. Ендеше осы екі жазық тық тың қ иылысқ ан тү зуінің бойындағ ы кез келген нү ктенің координаттары екі жазық тық тың да тең деуін қ анағ аттандырады. Сондық тан осы екі тең деулер жү йесін тү зудің жалпы тең деуі дейді.
5. Екі тү зудің арасындағ ы бұ рыш. Екі тү зу канондық тең деулерімен берілсін:
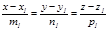 жә не
жә не 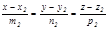 Екі тү зудің арасындағ ы бұ рыш, сол тү зулердің бағ ыттаушы векторларының арасындағ ы бұ рышқ а тең (
Екі тү зудің арасындағ ы бұ рыш, сол тү зулердің бағ ыттаушы векторларының арасындағ ы бұ рышқ а тең (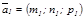 ,
,  ):
):
(5.10)
Егер тү зулер ө зара параллель болса, онда 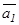 ||
||  болады. Тү зулердің параллелдік шарты:
болады. Тү зулердің параллелдік шарты:
 , егер тү зулер ө зара перпендикуляр болса, онда
, егер тү зулер ө зара перпендикуляр болса, онда 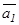
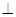
 болады. Тү зулердің перпендикулярлық шарты:
болады. Тү зулердің перпендикулярлық шарты:  болады.
болады.
Тү зу мен жазық тық. Жалпы тең деуімен берілген жазық тық 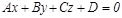 пен канондық тең деуімен тү зудің
пен канондық тең деуімен тү зудің 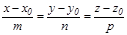 арасындағ ы бұ рышты табу керек.
арасындағ ы бұ рышты табу керек.
Тү зу мен жазық тық тың арасындағ ы бұ рыш деп, осы тү зу мен оның жазық тық қ а тү сірілген проекциясының арасындағ ы сыбайлас бұ рыштың біреуін айтады. Тү зу мен жазық тық тың арасындағ ы бұ рыштың синусы мына формуламен есептелінеді:
(5.11)
Тү зу мен жазық тық тың параллелдік белгісі: 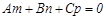 . Тү зу мен жазық тық тың перпендикулярлық белгісі:
. Тү зу мен жазық тық тың перпендикулярлық белгісі: