Екінші ретті қисықтар мен беттер. Екінші ретті қисықтар

Шең бер

Анық тама. Центр деп аталатын берілген нү ктеден бірдей қ ашық тық та жататын жазық тық тағ ы нү ктелердің геометриялық орындарын шең бер деп атайды.

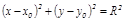
(6.1) – тең деуі центрі С 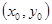нү ктесінде жатқ ан радиусы R -ге тең шең бердің тең деуі.

Егер шең бердің центрі С координаттардың бас нү ктесінде жатса, яғ ни 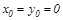болса, онда (6.1) мына тү рге келеді: (6.2)

Эллипс

Анық тама. Фокустар деп аталатын берілген екі нү ктеден қ ашық тық тарының қ осындысы тұ рақ ты шама болатын жазық тық тағ ы нү ктелердің геометриялық орындарын эллипс деп атайды.

Анық тама бойынша 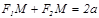, мұ ндағ ы 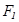жә не 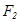- фокустар деп аталатын берілген нү ктелер, 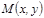-эллипстің бойындағ ы кез келген нү кте, 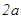-тұ рақ ты шама.

Егер 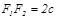десек, онда 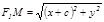, 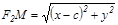. Енді осы мә ндерді 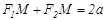тең деуіне қ ойып, тү рлендіріп, эллипстің канондық тең деуін аламыз:

мұ ндағ ы 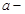эллипстің ү лкен жарты ө сі, 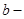оның кіші жарты ө сі болады. 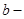ны табу ү шін эллипстің бойынан 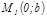нү ктесін аламыз. 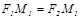болғ андық тан 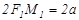немесе 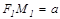болады. Пифагор теоремасы бойынша 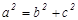. Осыдан 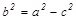деп белгілейміз. 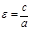қ атынасын эллипстің эксцентриситеті деп атайды. 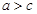болғ андық тан 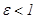. 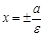эллипстің директрисаларының тең деуі. Ол эллипстің сыртында жатады.