Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Векторлардың сызықтық тәуелділігі. Базис
|
|
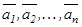 векторлар жү йесі берілсін.
векторлар жү йесі берілсін.
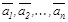 векторлар жү йесі ү шін бә рі бірдей нө лге тең емес жә не
векторлар жү йесі ү шін бә рі бірдей нө лге тең емес жә не
тең дігін қ анағ аттандыратын 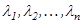 сандары табылса, онда
сандары табылса, онда 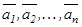 векторларын сызық тық тә уелді векторлар деп атайды. Ал егер
векторларын сызық тық тә уелді векторлар деп атайды. Ал егер 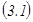 тең дік тек
тең дік тек 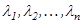 сандарының барлығ ы бірдей нө лге тең болғ анда ғ ана орындалса, онда
сандарының барлығ ы бірдей нө лге тең болғ анда ғ ана орындалса, онда 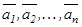 векторлар жү йесі сызық тық тә уелсіз деп аталады.
векторлар жү йесі сызық тық тә уелсіз деп аталады.
Егер 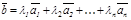 тең дігі орындалатын
тең дігі орындалатын 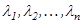 сандары табылса, онда
сандары табылса, онда 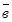 векторы
векторы 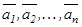 векторларының сызық тық комбинациясы деп аталады.
векторларының сызық тық комбинациясы деп аталады.
Теорема. Екі вектор сызық тық тә уелді болуы ү шін олардың ө зара коллинеар болуы қ ажетті жә не жеткілікті.
Бұ л теоремадан кез келген коллинеар емес екі вектор сызық тық тә уелсіз болады деген қ орытынды шығ ады.
Теорема. Ү ш вектор сызық тық тә уелді болуы ү шін олардың компланар болуы қ ажетті жә не жеткілікті. Бұ л теоремадан кез келген компланар емес ү ш вектор сызық тық тә уелсіз векторлар жү йесін қ ұ райды деген қ орытынды шығ ады. Егер жазық тық та кез келген 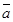 векторы ү шін
векторы ү шін 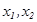 нақ ты сандары табылып, мына тең дік
нақ ты сандары табылып, мына тең дік  орындалса, онда белгілі ретпен алынғ ан
орындалса, онда белгілі ретпен алынғ ан 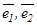 сызық тық тә уелсіз векторлар жұ бы жазық тық тағ ы базис деп аталады. Мұ ндағ ы
сызық тық тә уелсіз векторлар жұ бы жазық тық тағ ы базис деп аталады. Мұ ндағ ы 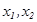 сандары
сандары 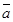 векторының
векторының 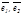 базисіндегі координаттары деп аталады да былай белгіленеді:
базисіндегі координаттары деп аталады да былай белгіленеді: 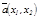 . Егер кең істікте кез келген
. Егер кең істікте кез келген 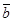 векторы ү шін
векторы ү шін 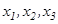 нақ ты сандары табылып, мына тең дік
нақ ты сандары табылып, мына тең дік 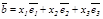 орындалса, онда белгілі ретпен алынғ ан сызық тық тә уелсіз
орындалса, онда белгілі ретпен алынғ ан сызық тық тә уелсіз 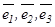 векторлар ү штігін кең істіктегі базис деп атайды. Мұ ндағ ы
векторлар ү штігін кең істіктегі базис деп атайды. Мұ ндағ ы 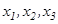 сандары
сандары 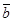 векторының
векторының 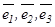 базисіндегі координаттары деп аталады да былай белгіленеді:
базисіндегі координаттары деп аталады да былай белгіленеді: 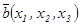 .
.
Базисті қ ұ раушы векторлар базистік векторлар деп аталады. Осы анық тамалар мен теоремалардан кез келген коллинеар емес екі вектор жазық тық та, ал кез келген компланар емес ү ш вектор кең істікте базистік векторлар жү йесі болады деген қ орытынды шығ ады.
Векторды координат ө стердің орттары арқ ылы жіктеу. Вектордың модулі. Кең істіктегі тік бұ рышты декарттық 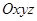 координаталар жү йесін қ арастырайық. Ох, Оу, Oz координат ө стерінің бойында жатқ ан бірлік (орт) векторларды сә йкесінше
координаталар жү йесін қ арастырайық. Ох, Оу, Oz координат ө стерінің бойында жатқ ан бірлік (орт) векторларды сә йкесінше 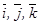 деп белгілейік. Сонда реттелген ү штік
деп белгілейік. Сонда реттелген ү штік 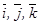 кең істікте базистік векторлар жү йесін қ ұ райды. Мұ ндай, базистік векторлар жү йесін ортогональ базистік жү йе (базис) деп атайды
кең істікте базистік векторлар жү йесін қ ұ райды. Мұ ндай, базистік векторлар жү йесін ортогональ базистік жү йе (базис) деп атайды 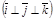 .
. 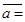
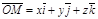 , себебі ү ш вектордың қ осындысы.
, себебі ү ш вектордың қ осындысы.
Бұ л формула 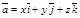 вектордың координат ө стерінің орттары арқ ылы жіктелген тү рі деп аталады немесе қ ысқ аша
вектордың координат ө стерінің орттары арқ ылы жіктелген тү рі деп аталады немесе қ ысқ аша 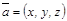 деп жазады.
деп жазады.
Екінші жағ ынан 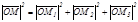 =
= 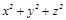 , Осыдан
, Осыдан 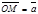 болғ андық тан
болғ андық тан 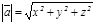 - вектордың модулі (ұ зындығ ы).
- вектордың модулі (ұ зындығ ы).
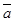
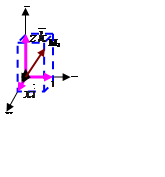 1-мысал. Егер
1-мысал. Егер 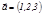 , онда
, онда 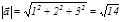 Егер
Егер 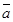 векторы Ох, Оу, Oz ө стерімен сә йкесінше
векторы Ох, Оу, Oz ө стерімен сә йкесінше 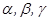 бұ рыштарын қ ұ рса, онда
бұ рыштарын қ ұ рса, онда
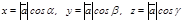 , осыдан
, осыдан 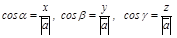 болады.
болады.
Мұ ндағ ы 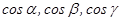 сандары
сандары 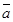 векторының бағ ыттаушы косинустары деп аталады. Алдың ғ ы ө рнекті вектордың модулінің формуласына қ ойып,
векторының бағ ыттаушы косинустары деп аталады. Алдың ғ ы ө рнекті вектордың модулінің формуласына қ ойып,
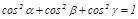 тең дігін аламыз.
тең дігін аламыз. 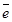 бірлік векторының коодинаттары
бірлік векторының коодинаттары 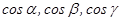 екенін оң ай байқ ауғ а болады. Сонымен,
екенін оң ай байқ ауғ а болады. Сонымен, 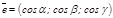 .
.
2-мысал. 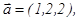 векторы ү шін
векторы ү шін