Сызықтық теңдеулер жүйесін шешу тәсілдері.

1. Крамер ережесі. n белгісізі бар n тең деулер жү йесі берілсін

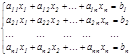Мұ ндай жү йенің А матрицасы квадрат матрица болады.

Теорема. Егер жү йесі ү шін 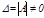болса, онда жү йенің жалғ ыз шешімі былайша табылады:

мұ нда 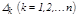- 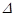анық тауышындағ ы 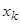белгісіздерінің коэффициеттерін бос мү шелермен алмастырғ аннан пайда болғ ан анық тауыш. Крамер формуласы деп аталады.

2. Матрицалық ә діс. n белгісізі бар n тең деулер жү йесі, яғ ни жү йе берілсін. Жү йені матрицалық тү рде былай жазамыз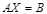

Теорема. Егер 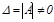болса, онда жү йесінің 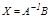тең дігімен анық талатын жалғ ыз шешімі бар.

3. Гаусс ә дісі. n белгісізі бар m тең деулер жү йесі, яғ ни 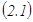берілсін. Жү йені Гаусс ә дісімен шешу екі кезең нен тұ рады. Бірінші кезең де (тік жү ріс) жү йе трапеция тә різдес тү рге келтіріледі.

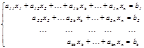– трапеция тә різдес жү йе.

Мұ нда 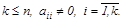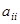коэффициенттері жү йенің негізгі элементтері деп аталады.

Екінші кезің де (кері жү ріс) мү мкін болса, шық қ ан жү йеден біртіндеп белгісіздерді табады. Практикада жү йемен емес кең ейтілген матрицамен істеген ың ғ айлы болады. Сондық тан жү йені Гаусс ә дісімен шешу ү шін кең ейтілген матрица қ ұ рып, оны элементарлық тү рлендірудің кө мегімен трапеция тә різдес тү рге келтіреді. Бұ л жағ дайда 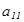коэффициентінің 1-ге тең болғ аны ың ғ айлы. Ол ү шін тең деулердің орындарын ауыстыру керек немесе тең деудің екі жағ ын да 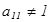бө лу керек. Содан соң қ айтадан жү йе қ ұ рып, сол жү йені шешеміз.

Теорема (Кронекер-Капелли) 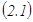жү йе ү йлесімді болуы ү шін жү йенің матрицасының рангі кең ейтілген матрицаның рангіне тең болуы қ ажетті жә не жеткілікіті, яғ ни .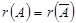