
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывность функции нескольких переменных
|
|
Пусть функция 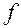 нескольких переменных задана в области
нескольких переменных задана в области 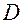 , точка
, точка 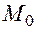 принадлежит
принадлежит 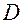 .
.
Определение. Функция 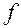 непрерывна в точке
непрерывна в точке 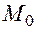 , если ее предел в этой точке равен значению функции в самой точке:
, если ее предел в этой точке равен значению функции в самой точке:
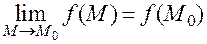 .
.
Это означает, что близким к 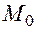 точкам
точкам 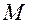 соответствуют близкие к
соответствуют близкие к  значения функции
значения функции 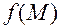 .
.
Определение. Функция 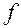 непрерывна в области
непрерывна в области 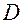 , если она непрерывна в каждой точке этой области.
, если она непрерывна в каждой точке этой области.
Для функции двух переменных 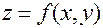 это геометрически означает, что поверхность графика функции
это геометрически означает, что поверхность графика функции 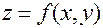 не имеет скачков, разрывов, является непрерывной в интуитивном смысле.
не имеет скачков, разрывов, является непрерывной в интуитивном смысле.
Аналогично определяется непрерывность в точке и области для функции большего числа переменных.
Теорема (критерий непрерывности в терминах приращений). Для того, чтобы функция 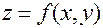 была непрерывна в точке
была непрерывна в точке 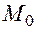 , необходимо и достаточно, чтобы бесконечно малым (стремящимся к нулю) приращениям независимых переменных
, необходимо и достаточно, чтобы бесконечно малым (стремящимся к нулю) приращениям независимых переменных 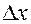 и
и 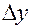 соответствовало бесконечно малое приращение функции:
соответствовало бесконечно малое приращение функции: 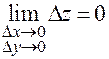 .
.
Доказательство. По свойствам предела:
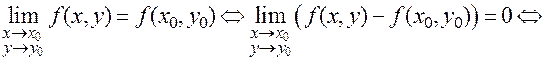
 . ▄
. ▄