Выбор наилучшей нелинейной регрессии по приведенному индексу детерминации

Цель работы. Используя пространственную выборку таблицы 2.1 и команду «Добавить линию тренда» построить шесть уравнений нелинейной регрессии (полиномиальное уравнение строится пр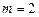и и 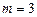), определить для каждого уравнения индекс детерминации 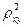(значение выводится), приведенный индекс детерминации 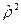(значение вычисляется) и по максимальному значению 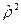найти наилучшее уравнение нелинейной регрессии.

Приведенный индекс детерминации. Индекс детерминации 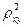характеризует близость построенной регрессии к исходным данным, которые содержат «нежелательную» случайную составляющую 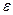. Очевидно, что, построив по данным таб. 2.1 полином 5-ого порядка, получаем «идеальное» значение 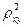=1, но такое уравнение содержит в себе не только независимую переменную 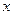, но составляющую 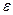и это снижает точность использования построенного уравнения для прогноза. Поэтому при выборе уравнения регрессии надо учитывать не только величину 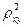, но и «сложность» регрессионного уравнения, определяемое количеством коэффициентов уравнения. Такой учет удачно реализован в так называемом приведенном индексе детерминации:

, (2.1)

где 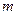- количество вычисляемых коэффициентов регрессии. Видно, что при неизменных увеличение 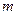уменьшает значение 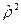. Если количество коэффициентов у сравниваемых уравнений регрессии одинаково (например, 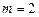), то отбор наилучшей регрессии можно осуществлять по величине 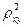. Если в уравнениях регрессии меняется число коэффициентов, то такой отбор целесообразно по величине .

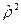Решение. Для построения каждого уравнения выполняем шаги 2 – 6 (для первого уравнения еще и шаг 1) и размещаем в одном документе шесть окон, в которых выводятся найденные уравнения регрессии уравнения и величина 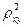. Затем формулу уравнения и 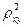заносим в таблицу 2.2. Далее по формуле (2.1) вычисляем приведенный индекс детерминации 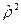и заносим эти значения также в таблицу (см. таб. 2.2).

Таблица 2.2

№	Уравнение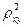
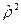
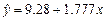
		0.949	0.938
		0.9916	0.9895
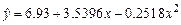	(полиноминальная, 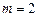)	0.9896	0.9827
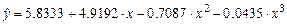	(полиноминальная, 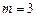)	0.9917	0.9792
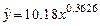
		0.9921	0.9901
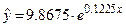
		0.9029	0, 8786

В качестве «наилучшего» уравнения регрессии выбираем уравнение, имеющее наибольшую величину приведенный коэффициент детерминации 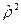. Из таб. 2.2 видно, что таким уравнением является степенная функции (в таблице строка с этой функцией выделена серым цветом)

,

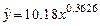имеющая величину 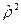= 0.9901.

Задание для самостоятельной работы.

1. Используя статистические данные по численности населения России выполнить построение «наилучшей» модели парной регрессии. Оценить численность населения в 2000 году.

2. Введя дополнительное данное: значение численности населения России в 1998 году 146, 2 млн. человек, уточнить экстраполяцию, используя только данные 90-х годов.