Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 3. ГЕТЕРОСКЕДАСТИЧНОСТЬ
|
|
Цель: научиться оценивать наличие эффекта гетероскедастичности.
Основные формулы и понятия:
Тест Парка
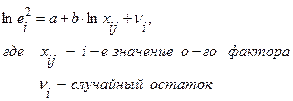
Условие принятия гипотезы: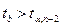 
Если данное условие выполняется, то нулевая гипотеза о наличии гетероскедастичности будет принята при уровне значимости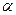 
.
Тест ранговой корреляции Спирмена
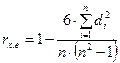— коэффициент ранговой корреляции Спирмена,
где x — одна из объясняющих переменных,
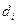— разность между рангом i-го наблюдения x и рангом модуля остатка в i-м наблюдении.
— статистика.
Если в модели регрессии имеется более одной объясняющей переменной, то проверка гипотезы может выполняться с использованием каждой из них.
Условие принятия гипотез: 
.
Если данное условие выполняется, то нулевая гипотеза об отсутствии гетероскедастичности отклоняется при уровне значимости .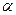
Для проведения теста ранговой корреляции Спирмена необходимо выполнить следующие действия:
1. Отсортировать данные в таблице по возрастанию значений x;
2. Придать каждому наблюдению ранг, для чего необходимо добавить новый столбец, в котором задать числа от 1 до n;
3. Вызвать из пакета анализа надстройку Регрессия, указав в диалоговом окне опцию Остатки. После выполнения данной надстройки появится дополнительная таблица, в которой содержатся номера наблюдений, прогнозы и остатки. Тот столбец таблицы, в котором находятся остатки, необходимо перенести к исходным данным. После выполнения этих действий наша таблица будет содержать четыре столбца: ранг наблюдения, упорядоченные значения регрессора x, значения y и значения остатков;
4. Отсортировать данные по возрастанию модулей остатков и добавить новый столбец рангов остатков, аналогичным образом задав значения от 1 до n;
5. В дополнительном столбце вычислить значения разности между двумя полученными рангами (это и будет значение Di);
6. На основании формул подсчитать коэффициент ранговой корреляции и статистику;
7. Проверить гипотезу.
Вид таблицы для проведения теста ранговой корреляции Спирмена
| Ранг по X | Цена X (р.) | Спрос Y (тыс. шт.) | Остатки | Ранг по остаткам | Разность рангов Di | Di * Di |
| 15, 91р. | 117, 088 | -0, 34387 | ||||
| 15, 54р. | 119, 864 | -0, 39014 | ||||
| 16, 76р. | 110, 023 | -0, 84306 | ||||
| 15, 21р. | 123, 809 | 1, 019821 | -2 | |||
| 15, 28р. | 121, 175 | -1, 11646 | -2 | |||
| 15, 92р. | 116, 17 | -1, 12322 | ||||
| 15, 95р. | 118, 344 | 1, 257187 | ||||
| 16, 69р. | 110, 106 | -1, 31194 | ||||
| 15, 09р. | 125, 178 | 1, 426776 | -8 | |||
| 15, 62р. | 118, 068 | -1, 5813 | -4 | |||
| 16, 31р. | 116, 201 | 1, 847847 | ||||
| 16, 33р. | 111, 457 | -2, 67328 | ||||
| 16, 60р. | 115, 103 | 3, 003645 | ||||
| 15, 49р. | 116, 914 | -3, 7319 | -10 | |||
| 15, 70р. | 123, 589 | 4, 559903 | -8 | |||
| Сумма |
Следовательно, значение ранговой корреляции Спирмена будет равно
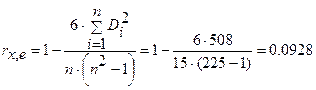
А значение статистики будет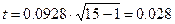 
Выбрав уровень значимости 5 %, получаем критическую точку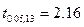 
. Данное значение получено формулой СТЬЮДРАСПОБР(0, 05; 13).
Поскольку условие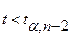 
не выполняется, то гипотеза о наличии гетероскедастичности будет принята.
Тест Гольдфельда — Кванта
В этом случае все наблюдения необходимо упорядочить по мере возрастания значений x. Разделить исходную модель на три равных части. Если количество наблюдение не делится нацело на 3, то уменьшается количество наблюдений в средней части, а первая и вторая части остаются одинаковыми по количеству наблюдений. Затем построить регрессионную модель для первых k и последних k наблюдений. Соответственно обозначим через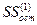 
и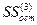 
необъясненную сумму квадратов отклонений в каждой регрессии. Тогда статистика имеет вид
.
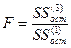Если выполняется условие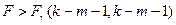 
, то гипотеза об отсутствии гетероскедастичности отвергается.