
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однофакторные дисперсионный анализ.
|
|
Задачу однофакторного дисперсионного анализа можно представить как проверку связи двух признаков, один из которых измеряется по интервальной шкале, а другой – по номинальной. Эта задача является логическим обобщением сравнения средних значений в группах на ситуацию, когда групп не две, а больше. Действительно, признак, измеряемый по номинальной шкале, делит всех респондентов на группы (число групп равно числу вариантов ответа). В каждой группе можно вычислить среднее значение того признака, который измеряется по интервальной шкале. Если связи между факторами нет, то во всех группах средние значения будут равны.
Вместе с тем, использование t-теста для решения такой задачи может привести к ошибкам. На первый взгляд, можно было бы сравнить средние значения в 1-й и 2-й группах, затем во 2-й и 3-й, в 1-й и 3-й, в 1-й и 4-й группах и т.д. Но таких этапов окажется достаточно много. Для 3-х вариантов ответа в номинальном признаке это всего 3 сравнения, для 4-х – уже 6, для пяти – 10, для шести – 15, для 7 – 21, и т.д.
Поэтому даже если все средние значения в популяции равны, только благодаря статистическому разбросу с достаточной вероятностью могут получиться достаточно большие отклонения, которые мы интерпретируем как значимые различия. Иными словами, если нам требуется провести 21 сравнение, то примерно в одной группе мы вынуждены будем отвергнуть гипотезу о равенстве средних значений на уровне значимости 0, 05 (или 5%, или 1/20). Поэтому дисперсионный анализ проверяет более строгое условие, формулируемое как нулевая гипотеза: «Средние значения во всех группах равны».
Технику проведения дисперсионного анализа рассмотрим на конкретном примере (по ходу вычислений будут даваться комментарии). Пусть у нас имеются данные о возрасте футболистов различного амплуа: защитников, полузащитников и нападающих (по 4 игрока каждой категории). Данные можно представить в виде такой таблицы:
| номер | защитники | полузащитники | нападающие |
Столбец «номер» введен только для удобства восприятия данных. Более того, в разных группах могло быть и различное число человек при условии, что дисперсии в группах (в популяции, а не по экспериментальным оценкам) должны быть равны: это требование дисперсионного анализа. В остальных трех столбцах в качестве значений фигурирует возраст игрока (в годах).
Данные могут быть представлены и по-другому, примерно в такой таблице:
| Амплуа игрока | З | З | Н | П | П | Н | З | П | П | Н | Н | З |
| Его возраст |
Вам не составит труда переписать данные из одной формы таблицы в другую.
Мы должны проверить гипотезу: «Средние возраста игроков всех амплуа равны». Первым делом средние значения надо вычислить (в каждой группе, а также в целом по выборке).
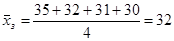
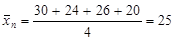
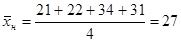
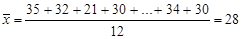
Далее, отклонение возраста каждого человека от среднего по выборке можно представить в виде суммы двух отклонений: отклонения его возраста от среднего значения в той группе (обозначим ее номер k), которой он принадлежит ( ), и отклонения этого среднего значения
), и отклонения этого среднего значения  от среднего по всей выборке (
от среднего по всей выборке (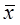 ):
):
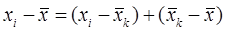
Для проверки наличия связи нужно определить, какие из членов вносят (в среднем по выборке) более существенный вклад. Первый член определяет разброс значений внутри групп. Второй – отклонения средних по группе значений от среднего значения по всей выборке. Если отклонения этих средних значений велики по сравнению с разбросом внутри групп, то различия между группами значимы и есть зависимость между признаками. Если же отличия средних в группах от среднего по популяции «тонут» в разбросе значений внутри групп, то мы принимаем гипотезу, что все средние значения равны.
Проиллюстрируем разброс средних значений графически (для трех групп):
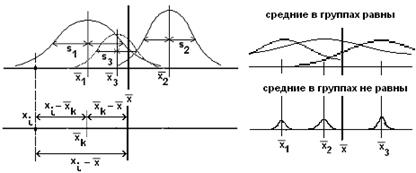
Дальнейшие вычисления методом дисперсионного анализа удобно проводить в таблицах. Первым делом получим общую сумму квадратов отклонений, равную по определению  . Формула для общей суммы напоминает дисперсию, поэтому методики вычисления этих величин слегка похожи. Сначала вычислим разности отклонений от среднего значения в популяции (которое равно 28):
. Формула для общей суммы напоминает дисперсию, поэтому методики вычисления этих величин слегка похожи. Сначала вычислим разности отклонений от среднего значения в популяции (которое равно 28):
| Амплуа: | защитник | полузащитник | нападающий | |
| разности | 35-28=7 | -7 | ||
| 32-28=4 | -4 | -6 | ||
| 31-28=3 | -2 | |||
| 30-28=2 | -8 |
Возводим ячейки таблицы в квадрат и суммируем:
| Амплуа: | защитник | полузащитник | нападающий | |
| Квадраты разностей | 72=49 | |||
| 42=16 | ||||
| Сумма по столбцу |
Суммируя нижнюю строку, получаем, что Sобщ=78+88+130=296
Далее требуется найти факторную сумму, равную по определению  , где k – число групп, а Nk - число испытаний в k-ой группе (в нашем примере во всех группах Nk=4). Факторная сумма для нашего примера равна:
, где k – число групп, а Nk - число испытаний в k-ой группе (в нашем примере во всех группах Nk=4). Факторная сумма для нашего примера равна:

Считаем факторную дисперсию, которая равна факторной сумме, деленной на (число групп - 1):
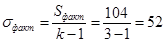
Остаточная сумма равна разности общей суммы и факторной:
Sост=Sобщ-Sфакт=296-104=192.
Остаточную сумму можно считать и по-другому, без вычисления общей суммы. По определению она равна сумме отклонений от среднего значения в той группе, которой принадлежит респондент:  . В нашем случае
. В нашем случае
Sост=(35-32)2+(32-32)2+(31-32)2+(30-32)2+(30-25)2+(24-25)2+…+(31-27)2=192.
Остаточная дисперсия равна: 
Для проверки гипотезы о том, что средние значения во всех группах равны, используется величина F, равная отношению факторной и остаточной дисперсий: 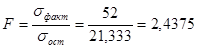
Если в популяции средние значения во всех группах действительно равны, то случайная величина F имеет F-распределение с числом степеней свободы, равным в числителе k-1, а в знаменателе N-k. В нашем случае это 3-1=2 и 12-3=9 степеней свободы, соответственно. Далее поступаем так же, как всегда при статистической проверке гипотез. Можно выбрать некоторый критический уровень значимости α, например, α =0, 05. После этого по таблице F-распределения (см. Приложение 5) c нужным числом степеней свободы можно определить критическое значение Fкрит. В данном случае для α =0, 05, d1=2 и d2=9 находим Fкрит=4, 26. Сравниваем экспериментальное значение F=2, 4375 с критическим значением Fкрит=4, 26. Поскольку F< Fкрит, мы принимаем нулевую гипотезу о равенстве всех средних значений. То есть, мы делаем вывод о том, что все средние значения в группах равны, а исследуемые признаки (факторы) не связаны между собой.
Если у Вас под рукой нет таблиц, но есть компьютер с наличием на нем Excel, для нахождения критического значения F по известному уровню значимости и степеням свободы можно воспользоваться функцией FРАСПОБР.
Можно проверять гипотезу и по-другому. По экспериментальному значению F и известным числам степеней свободы можно с помощью таблиц или функции Excel FРАСП определить экспериментальный уровень значимости α. В нашем примере он равен 0, 142575, или 14, 2572%. Далее по этой величине делают выводы о том, можем ли мы считать равными (различными) средние значения в группах. Как правило, считается, что связь между признаками есть, если уровень значимости меньше 0.05, или 5%. Более точные выводы о том, какой уровень значимости выбрать, решают экспериментаторы.