
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I. Похідна та її фізичний зміст
|
|
Самостійна робота №19-21
Тема: Логарифмічне диференціювання, диференціювання функцій заданих неявно, параметрично. Застосування похідної при розв’язуванні оптимізаційних задач
Мета: Відновити в пам’яті знання про похідну можливості застосовувати похідну у практичних розрахунках, виховувати тяжіння студентів до творчого мислення, практичної роботи.
Після вивчення теорії та виконання практичних завдань студент повинен знати всі етапи дослідження та побудови графіка функції, вміти досліджувати і будувати будь які графіки, розв’язувати оптимізаційні задачі.
I. Похідна та її фізичний зміст
Швидкість змінювання функції в точці 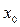 називають похідною функції в цій точці. Поняття похідної – одне з основних понять диференціального числення.
називають похідною функції в цій точці. Поняття похідної – одне з основних понять диференціального числення.
Границя відношення приросту функції 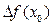 в точці
в точці 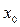 до приросту аргументу
до приросту аргументу  , коли останній прямує до нуля, називається похідною функції
, коли останній прямує до нуля, називається похідною функції 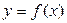 в точці
в точці 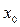 .
.
Похідну позначають так:
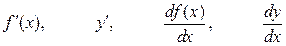 ,
,
тобто
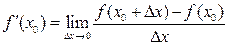 .
.
Якщо  – закон руху матеріальної точки, то
– закон руху матеріальної точки, то 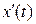 – її миттєва швидкість. У цьому і є механічний зміст похідної.
– її миттєва швидкість. У цьому і є механічний зміст похідної.