
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
IV. Диференціювання функцій
|
|
Диференціювання складної функції.
Нехай 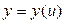 і
і 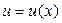 функції, що диференціюються. Тоді складна функція
функції, що диференціюються. Тоді складна функція 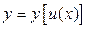 є також диференційована функція, причому
є також диференційована функція, причому
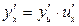 ,
,
чи 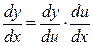 .
.
Це правило поширюється на ланцюжок з будь-якого кінцевого числа диференційованих функцій. Похідна складної функції дорівнює добутку похідних функцій, що її складають.
Приклад 1. 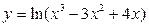
Положимо  , де
, де 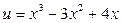 , тоді по формулі знайдемо
, тоді по формулі знайдемо
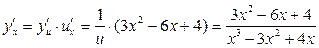
Приклад 2. 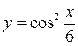
Положимо 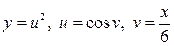 , знайдемо
, знайдемо

Логарифмічне диференціювання
Логарифмічна похідна функції 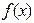 > 0 є похідною від логарифму даної функції
> 0 є похідною від логарифму даної функції 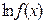 :
:
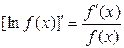 .
.
Обчислення логарифмічної похідної називається логарифмічним диференціюванням. Логарифмічне диференціювання застосовується при обчисленні похідної степенево-показникової функції, тобто функції виду
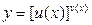 ,
,
а також при знаходженні похідної добутку декількох функції або похідної дробу.
Приклад 3. Обчислити похідну 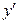 від функції
від функції 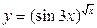 .
.
Знайдемо логарифм даної функції:
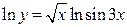 .
.
Диференціюючи обидві частини цієї рівності, отримуємо
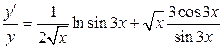 ,
,
звідки
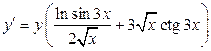 ,
,
або
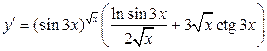 .
.