
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
VI. Похідна функції заданої параметрично
|
|
Якщо залежність функції 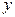 від незалежної змінної
від незалежної змінної 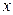 задана з допомогою допоміжної змінної (параметру)
задана з допомогою допоміжної змінної (параметру) 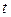 :
:
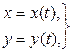
то
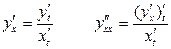 .
.
Приклад 5. Дана функція
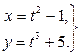
Знайти першу та другу похідну від 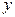 по
по 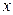 .
.
Маємо
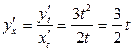 ,
,
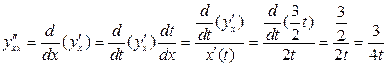 .
.
| В-нт | Завдання | |||
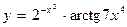
| 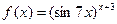
| 
| 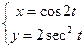
| |
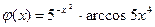
| 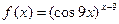
| 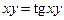
| 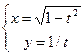
| |

| 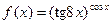
| 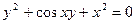
| 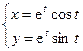
| |
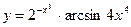
| 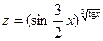
| 
| 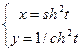
| |

| 
| 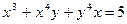
| 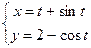
| |
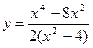
| 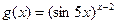
| 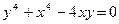
| 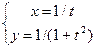
| |
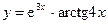
| 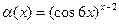
| 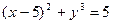
| 
| |
| 
| 
| 
| |

| 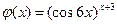
| 
| 
| |
| 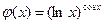
| 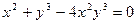
| 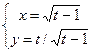
| |
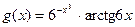
| 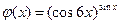
| 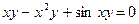
| 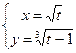
| |

| 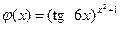
| 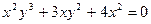
| 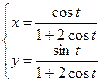
| |
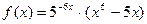
| 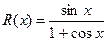
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| В-нт | Завдання | |||
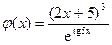
| 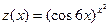
| 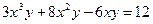
| 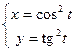
| |

| 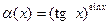
| 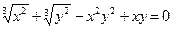
| 
| |
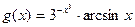
| 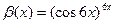
| 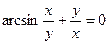
| 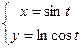
| |

| 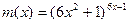
| 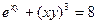
| 
| |
| 
| 
| 
| |
| 
| 
| 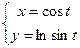
| |
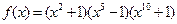
| 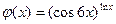
| 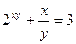
| 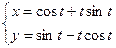
| |
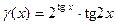
| 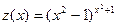
| 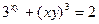
| 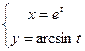
| |
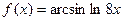
| 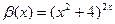
| 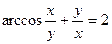
| 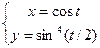
| |
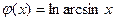
| 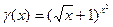
| 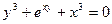
| 
|
ЗАДАЧА. Написати рівняння дотичної і нормалі до кривої у = х2 – х у точках її перетинання з віссю абсцис.
РІШЕННЯ. Знаходимо точки перетину кривої з віссю абсцис. Для цього вирішуємо рівняння у = 0:
х2 – х = 0; х/х - 1/=0;
х1 = 0 х2 = 1
Виходить, крива перетинає вісь абсцис у крапках О (0; 0) і А(1; 0).
Якщо y = f(x) – рівняння кривої, а М(х0; у0) – точка, що лежить на цій кривій, то рівняння дотичної до кривої в точці М має вигляд
у - y0=f’(x0)(x - x0)
а рівняння нормалі до кривої в точці М буде
y - y0= - 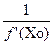 (x - x0)
(x - x0)
Тут f’(x0) 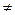 0
0
Знаходимо рівняння дотичної і нормалі до даної кривої в точці O(0; 0). Тому що f(x)=x2- x так як f’(x)=2x - 1
Тому рівняння дотичної:
у-0=(-1) (х - 0), так як у = -х;
Рівняння нормалі
у -0= - 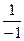 (х - 0), так як у = х.
(х - 0), так як у = х.
Потім знаходимо рівняння дотичної і нормалі до даної кривої в точці А(1; 0). Тому що х0 = 1, у0 = 0 f’(x0) =2 * 1 -1 = 1,
те рівняння дотичної
у - 0 = 1(х - 1), так як у = х - 1,
і рівняння нормалі
у - 0= -  (х - 0), тобто у = - х + 1.
(х - 0), тобто у = - х + 1.
Похідна, її геометричний і фізичний зміст.
Скласти рівняння дотичної і нормалі до даної кривої у зазначеній точці:
| В1 | y = x2–7x+3 x0 = 1 | В14 | y = 4sin6x x0 = 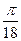
|
| В2 | y = x2–16x+7 x0 = 1 | В15 | y = 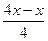 x0 = 2 x0 = 2
|
| В3 | y =  x0 = 8 x0 = 8
| В16 | y = x-x3 x0 = -1 |
| В4 | y = 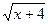 x0 = -3 x0 = -3
| В17 | y = 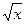 -3 -3 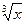 x0 = 64 x0 = 64
|
| В5 | y = x3–2x2+4x-7 x0 = 2 | В18 | y = 2x +  x0 = 1 x0 = 1
|
| В6 | y = x3-5x2+7x-2 x0 = 1 | В19 | y = 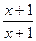 x0 = 1 x0 = 1
|
| В7 | y = x2-6x+2 x0 = 2 | В20 | y = 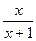 x0 = -2 x0 = -2
|
| В8 | y = 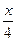 -x+5 x0 = 4 -x+5 x0 = 4
| В21 | y = 3 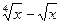 x0 = 1 x0 = 1
|
| В9 | y = 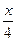 -27x+60 x0 = 2 -27x+60 x0 = 2
| В22 | y = 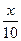 +3 x0 = 2 +3 x0 = 2
|
| В10 | y = - 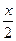 +7x - +7x - 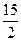 x0 = 3 x0 = 3
| В23 | y = 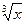 -20 x0 = -8 -20 x0 = -8
|
| В11 | y = 3tg2x+1 x0 = 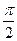
| В24 | y = -2(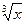 +3 +3 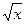 ) x0 = 1 ) x0 = 1
|
| В12 | y = 4tg3x x0 = 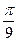
| В25 | y = 6x2-4x+2 x0 = -1 |
| В13 | y = 6tg5x x0 = 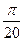
|