
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Программа по линейной алгебре
|
|
ЛИНЕЙНАЯ АЛГЕБРА
Контрольные задания и методические указания
Ростов-на-Дону
Печатается по решению кафедры фундаментальной и прикладной математики
Авторы-составители: доцент, к.т.н. Солопова О.Г.,
доцент, к.ф.-м.н. Рогожин С.В.
Рецензент: доцент, к.э.н. Алексейчик Т.А.
Контрольные задания и методические указания по дисциплине «Линейная алгебра» предназначены для самостоятельной работы студентов всех форм обучения. Дисциплина входит в федеральный государственный образовательный стандарт высшего профессионального образования всех направлений, содержащих курс математики.
Ростовский государственный экономический университет (РИНХ). 2011
КОНТРОЛЬНЫЕ ЗАДАНИЯ
И МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Контрольные задания и методические указания по дисциплине «Линейная алгебра» предназначены для студентов заочной формы обучения. Они могут быть использованы для более глубокого изучения раздела линейной алгебры, который входит в программу высшей математики всех направлений.
ВВЕДЕНИЕ
Студент должен владеть основными понятиями линейной алгебры в объеме программы, четко формулировать определения, уметь применять эти понятия при решении практических задач.
Студенты 1 курса заочного отделения должны выполнить по учебному плану одну контрольную работу своего варианта. Номер варианта совпадает с последней цифрой его учебного шифра (номер зачетной книжки). Номера задач вариантов контрольных работ указаны в таблице, приведенной ниже:
| номер варианта | Контрольная работа | ||||||||
| 81 91 101 | |||||||||
| 82 92 102 | |||||||||
| 83 93 103 | |||||||||
| 84 94 104 | |||||||||
| 85 95 105 | |||||||||
| 86 96 106 | |||||||||
| 87 97 107 | |||||||||
| 88 98 108 | |||||||||
| 89 99 109 | |||||||||
| 90 100 110 |
ИТОГОВЫЙ КОНТРОЛЬ ЗНАНИЙ: ЭКЗАМЕН.
Основные требования к итоговому контролю: знание основных понятий теории и умение их применять к решению практических задач.
Программа по линейной алгебре
1. Множества и операции над ними. Способы задания множеств. Пространства.
2. Отображения. Композиция отображений. Взаимно-однозначные отображения. Обратимые и обратные отображения.
3. Комплексные числа и алгебраические операции над ними. Комплексная плоскость, модуль и аргумент комплексного числа. Тригонометрическая и показательная формы комплексного числа.
4. Многочлены и алгебраические уравнения. Определения. Разложение многочлена. Основная теорема алгебры (теорема Гаусса) и ее следствия. Комплексные корни многочлена с действительными коэффициентами.
5. Системы линейных уравнений. Основные определения: решения, совместность, несовместность, определенность, неопределенность, равносильность систем. Однородные системы. Элементарные преобразования систем.
6. Методы Гаусса и Жордана-Гаусса решения систем линейных уравнений общего вида. Общее, частное, базисное решения; система, приведенная к единичному базису, базисные и свободные переменные. Ранг системы уравнений, максимальное число базисных решений. Жордановы исключения, их применения к решению систем линейных уравнений и отысканию базисных решений.
7. Матрицы и векторы. Основные определения. Линейные операции над векторами и матрицами. Частные виды матриц: квадратная, диагональная, единичная, строка, столбец. Произведение матриц и его свойства.
8. Операция транспонирования матриц и ее свойства.
9. Обратная матрица и ее построение.
10. Матричный оператор. Линейность матричного оператора. Композиция матричных операторов. Обратимость матричного оператора.
11. Матричная форма записи систем линейных уравнений и матричный способ ее решения.
12. Определители. Определители 2-го, 3-го и n -ого порядков: определение и основные свойства.
13. Разложение определителя по любому столбцу (строке). Теорема аннулирования.
14. Применение определителей к решению систем линейных уравнений. Теорема (формулы) Крамера.
15. Вырожденная, невырожденная матрицы. Критерий обратимости матрицы. Вычисление обратной матрицы через алгебраические дополнения.
16. Линейные векторные пространства. Определение векторного пространства. Аксиомы и следствия из них.
17. Линейная комбинация, линейная оболочка векторов. Линейная зависимость системы векторов: определения и основные свойства.
18. Размерность и базис векторного пространства. Критерий линейной независимости n векторов в 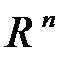 .
.
19. Координаты вектора в данном базисе. Разложение вектора по базису. Линейные операции над векторами в координатной форме.
20. Переход к новому базису. Матрица перехода от одного базиса к другому. Преобразование координат вектора при переходе к новому базису.
21. Линейные операторы. Образ и ядро линейного оператора, основные свойства. Матрица линейного оператора.
22. Операции над линейными операторами, действующими в фиксированном пространстве: сумма, умножение на число, произведение. Обратный оператор и его матрица.
23. Собственные значения и собственные векторы линейного оператора. Определение, процедура их отыскания. Методы приведения матрицы линейного операторы к диагональному виду.
24. Евклидово пространство. Скалярное произведение в 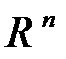 . Норма вектора. Неравенство Коши-Буняковского, неравенство треугольника. Угол между векторами. Ортогональные и ортонормированные базисы.
. Норма вектора. Неравенство Коши-Буняковского, неравенство треугольника. Угол между векторами. Ортогональные и ортонормированные базисы.
25. Линейные операторы в евклидовом пространстве. Самосопряженные операторы и их матрицы. Свойства самосопряженного оператора.
26. Линейные функционалы: определения, примеры. Теоремы об общем виде линейных функционалов.
27. Квадратичные формы: определения, примеры. Квадратичная форма в 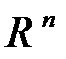 , ее матрица. Приведение квадратичной формы к сумме квадратов (каноническому виду). Знакоопределенность квадратичных форм.
, ее матрица. Приведение квадратичной формы к сумме квадратов (каноническому виду). Знакоопределенность квадратичных форм.
28. Линейные геометрические объекты. Гиперплоскость в 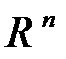 : общее уравнение; нормальный вектор и его свойства, частные виды уравнений. Прямая в
: общее уравнение; нормальный вектор и его свойства, частные виды уравнений. Прямая в 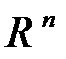 : параметрическое, каноническое, общее уравнение; уравнение по двум точкам.
: параметрическое, каноническое, общее уравнение; уравнение по двум точкам.
29. Прямая и гиперплоскость в 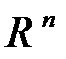 : углы, условия параллельности и ортогональности гиперплоскостей, прямых и друг с другом.
: углы, условия параллельности и ортогональности гиперплоскостей, прямых и друг с другом.
30. Расстояния между двумя точками, от точки до гиперплоскости. Уравнение отрезка и его середина.
31. Прямая линия на плоскости: общее уравнение и с угловым коэффициентом. Построение прямой линии по общему уравнению.
32. Гиперповерхности уровня линейных функционалов и квадратичных форм. Кривые второго порядка.
33. Выпуклые множества. Системы линейных неравенств Линейные задачи оптимизации, графический способ их решения.
34. Задача оптимального планирования. Задача о диете Постановка, математическая модель.
35. Формы задач линейного программирования (з.л.п.). Связь между ними. Запись з.л.п. в матричной форме.
36. Допустимое, оптимальное, опорное решения, область допустимых решений. Основные утверждения линейного программирования.
37. Вырождение, зацикливание, неразрешимость задач линейного программирования.
38. Симплексный метод решения задачи линейного программирования. Переход от опорного плана к оптимальному плану.
39. Построение исходного опорного решения.
40. Решение з.л.п. в общей или канонической форме.
41. Понятие о целочисленном программировании.
42. Метод Гомори решения задач целочисленного программирования.
43. Симметричные двойственные задачи. Достаточный признак оптимальности двойственных задач.
44. Симплексные преобразования в симметричных двойственных задачах.
45. Первая (основная) и вторая теоремы теории двойственности.
46. Экономический смысл двойственных переменных (показатель дефицитности ресурсов и влияния ограничений на значение целевой функции; показатель эффективности производства отдельных видов продукции с позиций критерия оптимальности и инструмент балансировки суммарных затрат и прибыли).
47. Постановка двойственной задачи в общей форме.
48. Анализ решения з.л.п. с использованием теории двойственности.
49. Транспортная задача. Постановка и математическая модель.
50. Условие разрешимости транспортной задачи. Ранг системы ограничений транспортной задачи.
51. Метод потенциалов. Критерий оптимальности транспортной задачи.
Улучшение опорного плана транспортной задачи.
52. Дисбаланс (открытая модель) и вырождение в транспортной задаче.
53. Задача о назначении.
54. Основные понятия теории игр.
55. Сведение матричной игры к задаче линейного программирования.
| № | Перечень основной и дополнительной литературы, методических разработок. |
| Основная литература: | |
| Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. М.: АСтрель: АСТ, 2007. -.425 с. | |
| 2. | Высшая математика для экономистов. Учеб. Для вузов/под ред. Н.Ш. Кремера. М.: ЮНИТИ-ДАНА, 2008.-.342 с. |
| 3. | Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. Часть 1, 2: М.: Высшая школа. 1982.-.272, 320 с. |
| 4. | Практикум по высшей математике для экономистов. Учебное пособие для вузов/под ред.Н.Ш. Кремера. М.: ЮНИТИ-ДАНА, 2005. -354с |
| 5. | Солопова О.Г.Линейная алгебра. Учебное пособие/РГЭУ «РИНХ».-Ростов н/Д, 2005. -.165с. |
| 6. | Высшая математика для экономических специальностей (ч.1, 2) учеб. и практикум/ под ред.Н.Ш. Кремера. М.: Высш. образование, 2008. – 344, 410 с |
| 7. | Данко П.Е. Высшая математика в упражнениях и задачах в 2 ч. М.: ОНИКС-21 век. Мир и образование, 2005.- 304, 415 с. |
| 8. | Минорский В.П. Сборник задач по высшей математике.- М.: Изд-во Физ.-мат. лит., 2005.-.352 с |
| 9. | Математические методы и модели исследования операций. Учебник для вузов./ под ред. Колемаева В.А. ЮНИТИ-ДАНА, 2008. -405 с. |
| 10. | Хемди А. Таха. Введение в исследование операций. Издательский дом «Вильямс, 2007. – 912 с. В библиотеке. |
| 11. | Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М.: Высшая школ., 1976. – 319 с. |
| 12. | Самаров К.Л. Задачи с решениями по высшей математике и математическим методам в экономике. М: Дашков и К, 2007. -424 с. |
| 13. | Решение оптимизационных задач в экономике. Уч. Пособие./под ред.Овечкина Е.В. и др. Ростов-на-Дону, Феникс, 2007. – 456 с. |
| 14. | Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики. СПб. Питер, 2006.- 367 с. |
| 15. | Абчук В.А. Экономико-математические методы. Элементарная математика. Методы исследования операций. Спб. Союз, 1999. –421 с. |
| 16. | Шапкин А.С., Мазаева Н.П. Математические методы и модели исследования операций. М.: Дашков и К, 2006. -478 с. |
| Дополнительная литература: | |
| 1. | Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. Учебник.-М.: МГУ, изд-во «ДИС», 1998.-468 с. |
| 2. | Ильин В.А., Куркина А.В. Высшая математика. М.: Проспект, 2007. -348с. В наличии в библиотеке. |
| 3. | Солопова О.Г., Яхненко Е.Л. Методические указания и учебные задания для текущего контроля изучения темы: Линейная алгебра./РИНХ, 1988. -34с.. |
| 4. | Солопова О.Г.Линейная алгебра. Контрольные задания и методические указания/РГЭУ «РИНХ», -Ростов н/Д, 2005.-37 с. |
| 5. | Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении. М.: Дело, 2002.-440 с. В наличии в библиотеке. |
| 6. | Фомин Г.П. Математические методы и модели в коммерческой деятельности. М.: Финансы и статистика, 2001. -544 с. |