Решение. 1. Построим область допустимых решений (ОДР).

1. Построим область допустимых решений (ОДР).

· Неравенства 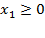и 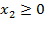задают первую координатную четверть в плоскости Ох₁х₂.

· Неравенство 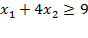определяет полуплоскость, ограниченную прямой

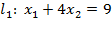, которую построим по двум точкам (9; 0) и (1; 2).

Определим, какая полуплоскость удовлетворяет неравенству – выберем на плоскости контрольную точку КТ (любую точку, не принадлежащую прямой), и подставим её координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением и полуплоскость, содержащая точку, тоже удовлетворяет неравенству. Если неравенство ложно, то искомая полуплоскость лежит с другой стороны от прямой. Для подстановки в неравенство удобно использовать начало координат.

Подставим 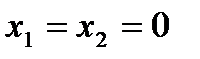в исходное неравенство .

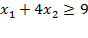Получим 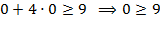. Данное утверждение является ложным, следовательно, неравенству 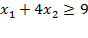соответствует полуплоскость, лежащая с другой стороны от прямой .

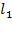· Построим полуплоскость, определяемую неравенством 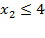. Строим ограничивающую ее прямую 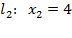, проходящую через точки (0; 4) и (3; 4). В качестве КТ возьмем 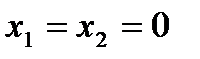и подставим её координаты в исходное неравенство 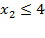: 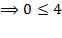- истина, значит, искомая полуплоскость лежит с той же стороны от прямой 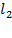, что и КТ.

· Неравенство 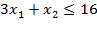определяет полуплоскость, ограниченную прямой 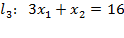, которая проходит через точки (5; 1) и (3; 7). Координаты КТ 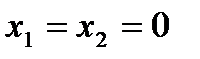подставим в исходное неравенство. Так как 3· 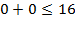истинно, то неравенству 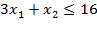соответствует полуплоскость, лежащая той же стороны от прямой 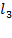, что и КТ.

Пересечение всех построенных полуплоскостей определяет область допустимых решений: четырехугольник АВСД

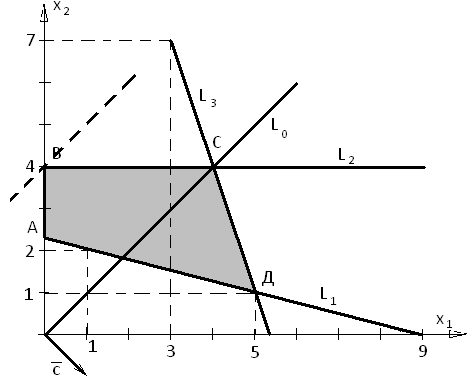
2. Построим линию уровня целевой функции.

Приравняем целевую функцию 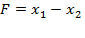к постоянной величине : 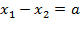. Пусть для удобства 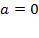, тогда уравнение линии нулевого уровня имеет вид

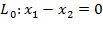. Построим ее по двум точкам (0; 0) и (1; 1).

3. Построим вектор целевой функции (градиент, вектор нормали). Так как функция цели линейная, координаты вектора определяются коэффициентами этой функции:

, .

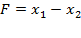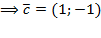При этом начало вектора находится в точке (0, 0), а концом вектора является точка .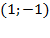

Если построения выполнены правильно, то линия уровня целевой функции и градиент перпендикулярны.

4. Определим оптимальное решение задачи.

Для решения задачи на минимум переместим линию нулевого уровня 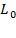параллельно самой себе в направлении, противоположном вектору до выхода ее из ОДР. Крайняя точка при этом является разрешающей, т.е. в ней находится оптимальный план.

В нашей задаче разрешающей является точка В c координатами .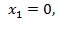

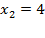Значение целевой функции в этой точке равно .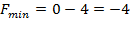

При решении задачи на максимум надо передвигать линию нулевого уровня 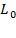параллельно самой себе в направлении вектора до выхода ее из ОДР. Крайняя точка Д (c координатами 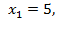. при этом является разрешающей, т.е. в ней находится оптимальный план. Значение целевой функции в точке Д равно .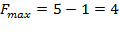

Ответ. Минимальное значение целевой функции достигается в точке 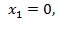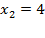и равно -4. Максимальное значение целевой функции достигается в точке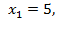 и равно 4.