
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 2. Теория двойственности
|
|
В предлагаемой альтернативной хозяйственной ситуации получите с помощью средств MS Excel (надстройка Поиск решения) оптимальный план производства продукции, проведите экономико-математический анализ оптимального плана с помощью двойственных оценок.
Предприятие выпускает три сорта мороженого: «Шоколадный пломбир», «Белочка» и «Лакомка» и реализует его по цене 57, 53 и 55 руб. за килограмм соответственно. Для производства используются три вида сырья. Расход сырья на производство одного килограмма мороженого и его запасы приведены в таблице:
| Сырье | Запас Сырья (кг.) | Расход сырья на производство 1кг. мороженого | ||
| «Шоколадный пломбир» | «Белочка» | «Лакомка» | ||
| Молоко | 0, 6 | 0, 7 | 0, 6 | |
| Масло | 0, 2 | 0, 2 | 0, 3 | |
| Шоколад | 0, 2 | 0, 1 | 0, 1 |
Требуется:
Сформулировать прямую оптимизационную задачу на максимум прибыли от реализации продукции, получить оптимальный план выпуска продукции.
Построим математическую модель прямой задачи.
Введем управляющие переменные:
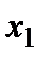 - количество произведенного мороженого «Шоколадный пломбир» (кг.),
- количество произведенного мороженого «Шоколадный пломбир» (кг.),
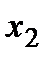 - количество произведенного мороженого «Белочка» (кг.),
- количество произведенного мороженого «Белочка» (кг.),
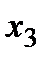 - количество произведенного мороженого «Лакомка» (кг.).
- количество произведенного мороженого «Лакомка» (кг.).
Построим функцию цели. Если реализовать 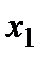 кг мороженого по цене 57 руб./кг, то прибыль составит
кг мороженого по цене 57 руб./кг, то прибыль составит 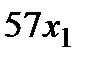 руб. и т.д. Следовательно, целевая функция - прибыль предприятия – запишется выражением
руб. и т.д. Следовательно, целевая функция - прибыль предприятия – запишется выражением
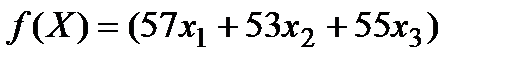 .
.
Исходя из требования максимизации прибыли:
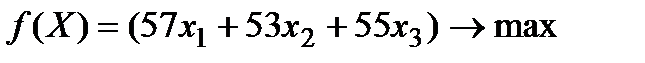 .
.
Построим систему ограничений. Расход каждого вида сырья определяется выражением:
для молока - 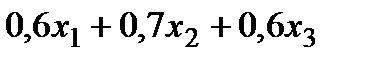 ,
,
для масла - 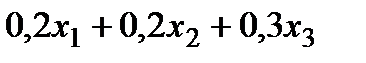 ,
,
для шоколада - 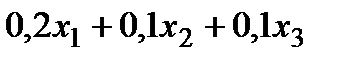 .
.
Так как расход сырья не может превышать количества, которым располагает предприятие, получим систему неравенств:
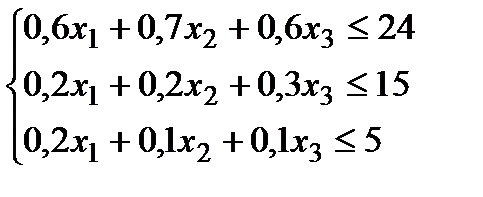
По смыслу задачи ясно, что переменные могут принимать лишь неотрицательные значения, т.е. 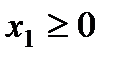 ,
, 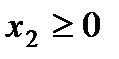 и
и 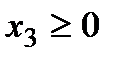 .
.
Теперь можно сформулировать математическую модель задачи:
найти 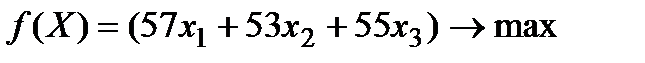
при ограничениях: 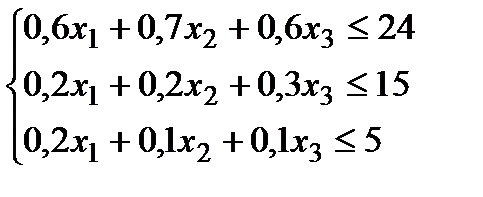 ,
,
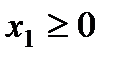 ,
, 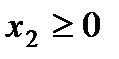 и
и 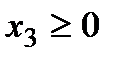 .
.
Решим задачу с помощью программы Excel «Поиск решения».
Подготовим форму: введем исходные условия задачи, зависимости для целевой функции и левых частей ограничений. Запустим программу Поиск решений.
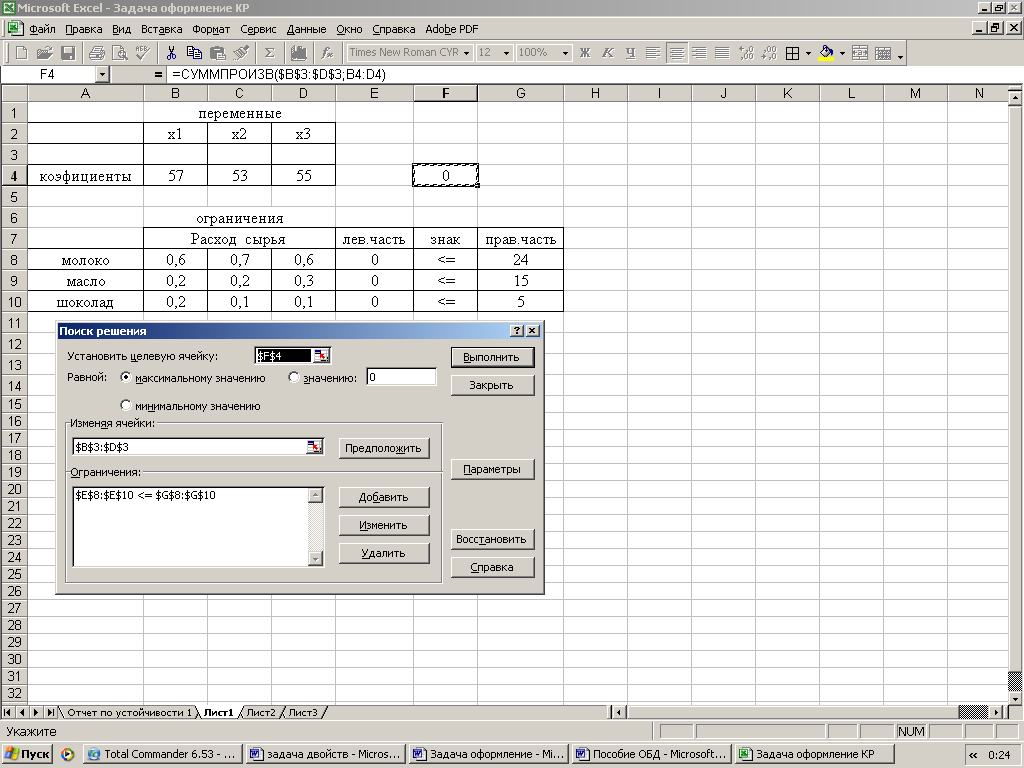
Результат поиска решения:
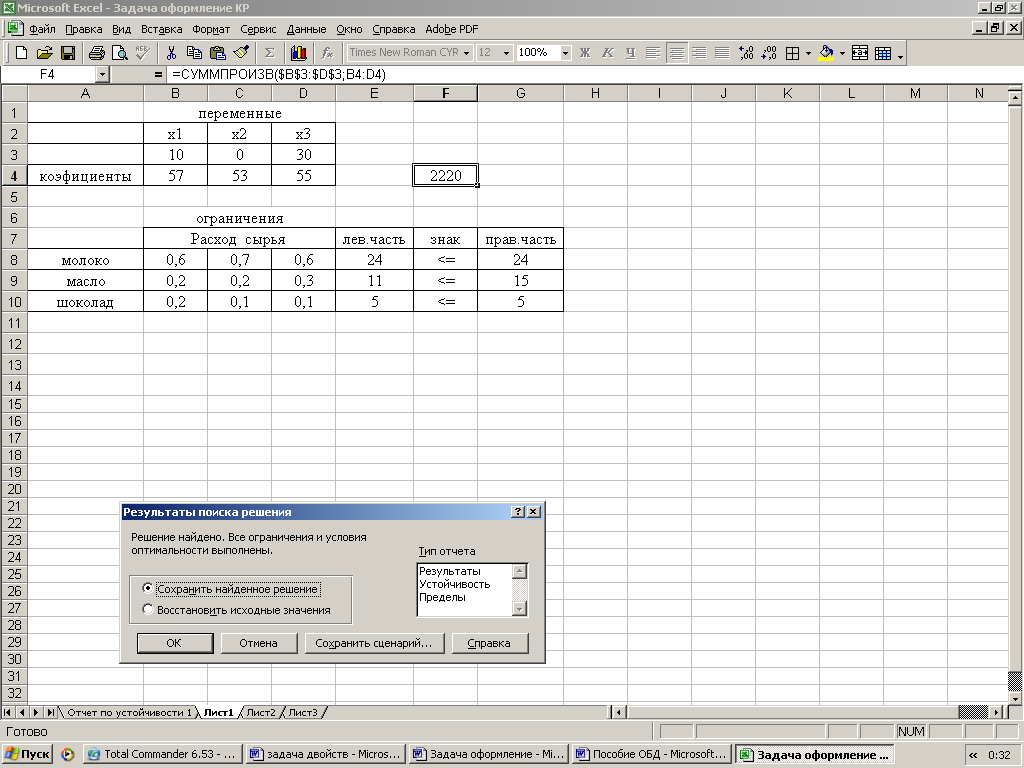
В результате решения задачи найден оптимальный план 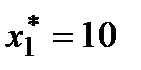 ,
, 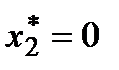 и
и 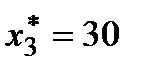 . При этом
. При этом  .
.
Ответ: максимальная прибыль составит 2220 руб. и будет получена при выпуске 10 кг. мороженого «Шоколадный пломбир» и 30 кг. мороженого «Лакомка».
Сформируем отчет по устойчивости.
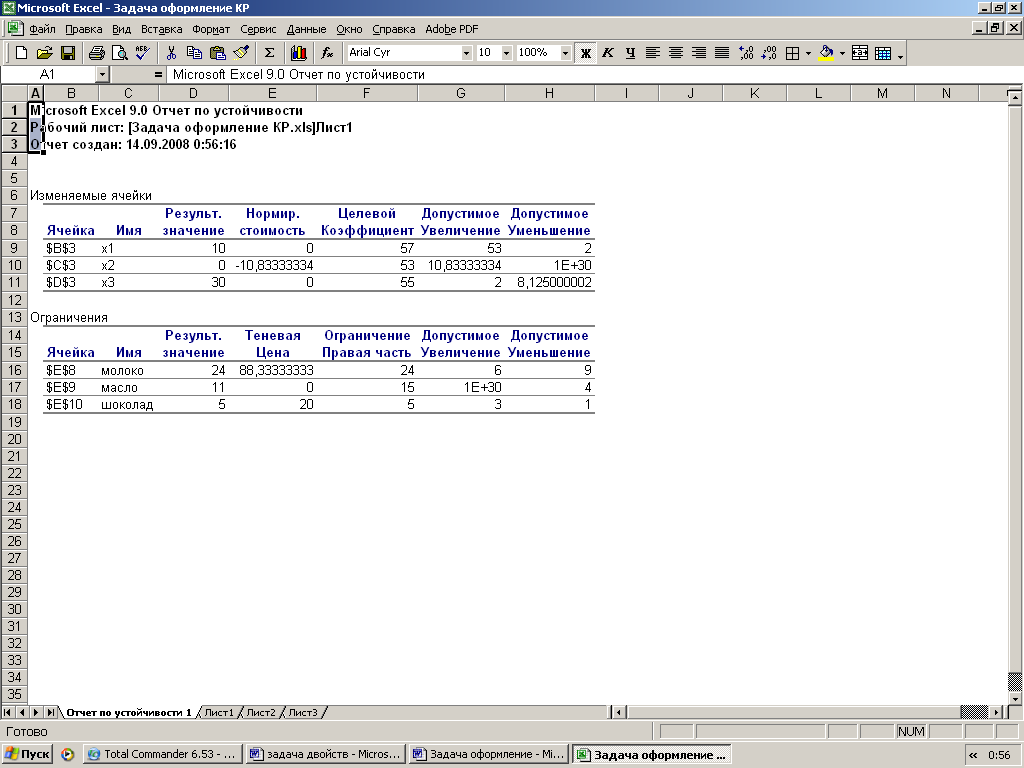
Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Применим правила построения модели двойственной задачи:
1. Число переменных в двойственной задаче равно числу ограничений исходной задачи. Введем обозначения: 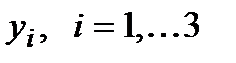 - двойственная оценка
- двойственная оценка 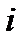 -го сырья. Все переменные
-го сырья. Все переменные 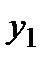 ,
, 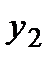 и
и 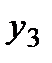 неотрицательны.
неотрицательны.
2. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены системы ограничений прямой задачи 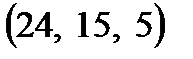 .
.
3. Прямая задача – на максимум, следовательно, двойственная к ней – на минимум: 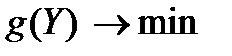 .
.
4. Число ограничений в двойственной задаче равно числу переменных в прямой – 3.
5. В прямой задаче все неравенства в системе ограничений имеют вид «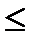 », следовательно, в двойственной задаче – вид «
», следовательно, в двойственной задаче – вид «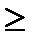 ».
».
6. Матрицы ограничений исходной и двойственной задач являются транспонированными друг к другу:
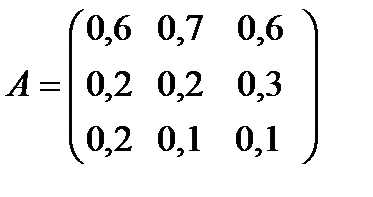
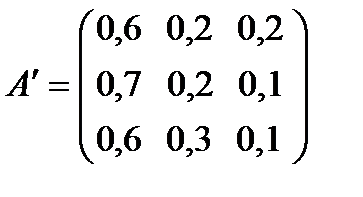
7. Правыми частями в ограничениях двойственной задачи являются коэффициенты при неизвестных в целевой функции исходной задачи 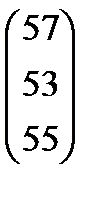 .
.
Учитывая эти правила, запишем модель двойственной задачи:
найти 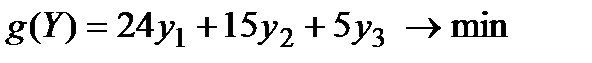
при ограничениях 
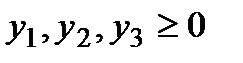 .
.
Значения двойственных оценок находятся в отчете по устойчивости в столбце «Теневая цена»: 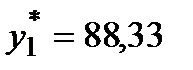 ,
, 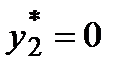 и
и 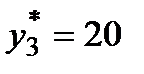
Вычислим значение целевой функции двойственной задачи:
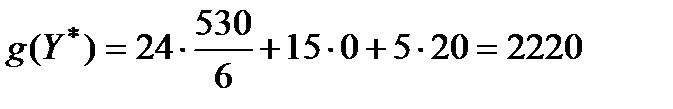
Как и должно быть в соответствии с Теоремой 1, экстремальные значения целевых функций прямой и двойственной задач совпадают, значит, оптимальный план двойственной задачи найден верно.
Пояснить нулевые значения переменных в оптимальном плане.
Рассмотрим оптимальное решение прямой задачи: 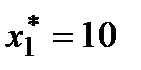 ,
, 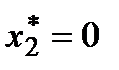 и
и 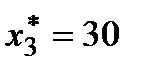 .
.
Компоненты оптимального решения основной задачи 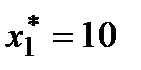 и
и 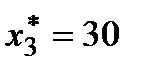 положительны, следовательно, два вида мороженого «Шоколадный пломбир» и «Лакомка» рентабельны и их следует производить в указанном количестве. Непроизводительных затрат нет, так как выполняется равенство
положительны, следовательно, два вида мороженого «Шоколадный пломбир» и «Лакомка» рентабельны и их следует производить в указанном количестве. Непроизводительных затрат нет, так как выполняется равенство 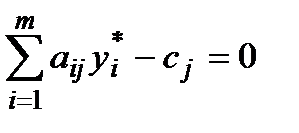 ,. Действительно:
,. Действительно:
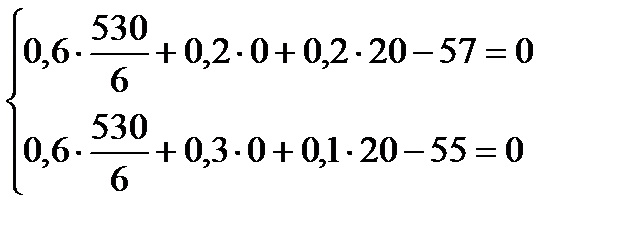
Нулевое значение 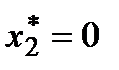 означает, что производство мороженого «Белочка» нерентабельно, величина непроизводительных затрат при этом
означает, что производство мороженого «Белочка» нерентабельно, величина непроизводительных затрат при этом 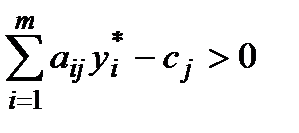 . Действительно
. Действительно 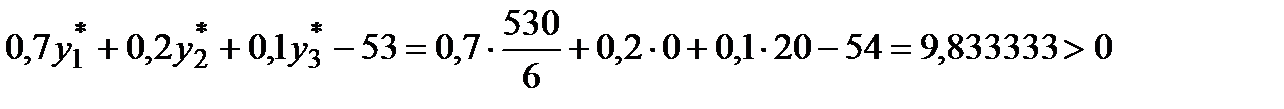 . Значит, изготовление 1 кг. мороженого «Белочка» будет снижать достигнутый оптимальный уровень прибыли на 9, 833333 руб.
. Значит, изготовление 1 кг. мороженого «Белочка» будет снижать достигнутый оптимальный уровень прибыли на 9, 833333 руб.
4. На основе двойственных оценок и теорем двойственности:
· проанализировать использование ресурсов в оптимальном плане исходной задачи;
Рассмотрим оптимальное решение двойственной задачи  ,
, 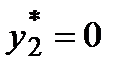 и
и 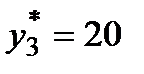 .
.
o Нулевая компонента 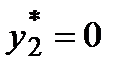 указывает, что ресурс масло – недефицитный, он используется не полностью. По теореме 2 выполняется неравенство
указывает, что ресурс масло – недефицитный, он используется не полностью. По теореме 2 выполняется неравенство 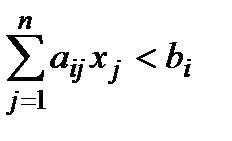 и излишки этого ресурса составляют
и излишки этого ресурса составляют 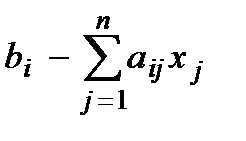
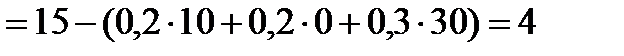 кг. Увеличение запаса ресурса масло не повлияет на величину прибыли.
кг. Увеличение запаса ресурса масло не повлияет на величину прибыли.
o Ненулевые значения 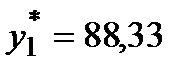 и
и 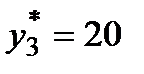 означают, что ресурсы молоко и шоколад являются дефицитными, они полностью используются в оптимальном плане и таким образом сдерживают рост функции цели. Действительно, по теореме 2 выполняется равенство
означают, что ресурсы молоко и шоколад являются дефицитными, они полностью используются в оптимальном плане и таким образом сдерживают рост функции цели. Действительно, по теореме 2 выполняется равенство 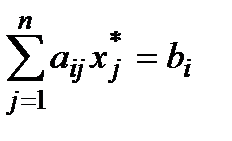 :
:
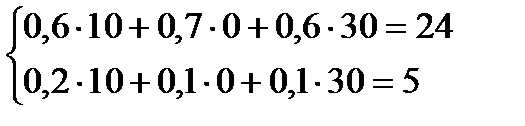 .
.
o Ресурс молоко является более дефицитным, чем ресурс шоколад, так как его двойственная оценка выше: 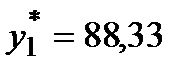

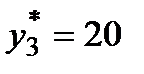 . Кроме того, каждый дополнительный килограмм молока, введенный в производство, позволит увеличить прибыль на 88, 333 руб., а каждый дополнительный килограмм шоколада – на 20 руб.
. Кроме того, каждый дополнительный килограмм молока, введенный в производство, позволит увеличить прибыль на 88, 333 руб., а каждый дополнительный килограмм шоколада – на 20 руб.
o Относительная заменяемость ресурсов молоко и шоколад определяется соотношением 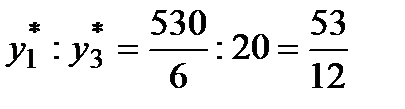 , т.е. 53 дополнительные единицы ресурса шоколад в плане получения прибыли равноценны 12-ти дополнительным единицам ресурса молоко т.к. по теореме об оценках
, т.е. 53 дополнительные единицы ресурса шоколад в плане получения прибыли равноценны 12-ти дополнительным единицам ресурса молоко т.к. по теореме об оценках 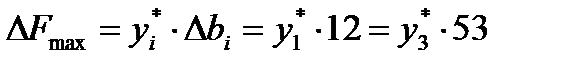
· определить, как изменится выручка от реализации продукции и план ее выпуска при увеличении запасов шоколада на 2 кг;
Анализ чувствительности решения к изменению запасов сырья проведем с помощью отчета по устойчивости.
Для запасов ресурса шоколад допустимое увеличение равно 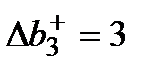 , допустимое уменьшение
, допустимое уменьшение  . По условию задачи запас шоколада предполагается увеличить на 2 кг., что соответствует значению
. По условию задачи запас шоколада предполагается увеличить на 2 кг., что соответствует значению 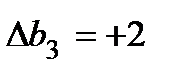 . Это изменение входит в интервал устойчивости, значит можно применить теорему об оценках
. Это изменение входит в интервал устойчивости, значит можно применить теорему об оценках  :
:
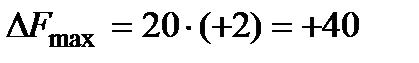 .
.
Вывод: при увеличении запаса шоколада на 2 кг прибыль увеличится на 40 руб.
· оценить целесообразность включения в план двух новых сортов мороженого «Малышок» и «Арбат» ценой 63 и 54 руб./кг соответственно.Расход сырья на производство одного килограмма мороженого приведен в таблице:
| Сырье | Расход сырья на производство 1кг | |
| «Малышок» | «Арбат» | |
| Молоко | 0, 8 | 0, 5 |
| Масло | 0, 15 | 0, 2 |
| Шоколад | 0, 05 | 0, 3 |
Рассчитаем критерий эффективности включения в производство новых сортов мороженого 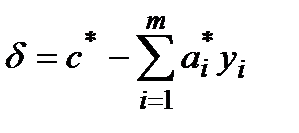 :
:
для мороженого «Малышок»:
 производство продукции невыгодно. Заметим, что производство этого сорта мороженого станет рентабельным, если прибыль от ее реализации составит не менее 71, 664 руб./кг.
производство продукции невыгодно. Заметим, что производство этого сорта мороженого станет рентабельным, если прибыль от ее реализации составит не менее 71, 664 руб./кг.
Для мороженого «Арбат»:
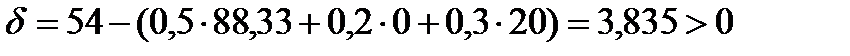 производство этого сорта мороженого выгодно.
производство этого сорта мороженого выгодно.